
已知一次函数
(1) 为何值时,
为何值时, 随
随 的增大而减小?
的增大而减小?
(2) 为何值时,它的图象经过原点?
为何值时,它的图象经过原点?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
如图,一次函数y=3x的图象与反比例函数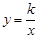 的图象的一个交点为A(1,m).
的图象的一个交点为A(1,m).
(1)求反比例函数 的解析式;
的解析式;
(2)若点P在直线OA上,且满足PA=2OA,直接写出点 的坐标(不写求解过程).
的坐标(不写求解过程).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图, 的图象与反比例函数
的图象与反比例函数 的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).
的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).
(1)求这两个函数的表达式;
(2)请直接写出当x取何值时,y1>y2.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
华盛印染厂生产某种产品,每件产品出厂价为30元,成本价为20元(不含污水处理部分费用).在生产过程中,平均每生产1件产品就有0.5立方米污水排出,所以为了净化环境,工厂设计了两种对污水进行处理的方案并准备实施.
方案一:工厂污水先净化处理后再排出,每处理1立方米污水所用的原料费用为2元,并且每月排污设备损耗等其它各项开支为27000元.
方案二:将污水排放到污水处理厂统一处理,每处理1立方米污水需付8元排污费.
(1)若实施方案一,为了确保印染厂有利润,则每月的产量应该满足怎样的条件?
(2)你认为该工厂应如何选择污水处理方案?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图所示,四边形OABC是矩形,点D在OC边上,以AD为折痕,将△OAD向上翻折,点O恰好落在BC边上的点E处,若△ECD的周长为2,△EBA的周长为6.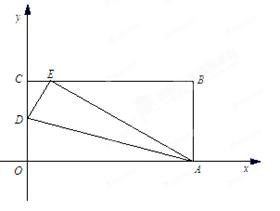
(1)矩形OABC的周长为 ;
(2)若A点坐标为 ,求线段AE所在直线的解析式.
,求线段AE所在直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(12分)汽车油箱中的余油量Q(升)是它行驶的时间 (小时)的一次函数.某天该汽车外出时,油箱中余油量与行驶时间的变化关系如图:
(小时)的一次函数.某天该汽车外出时,油箱中余油量与行驶时间的变化关系如图:
(1)根据图象,求油箱中的余油Q与行驶时间 的函数关系.(7分)
的函数关系.(7分)
(2)从开始算起,如果汽车每小时行驶40千米,当油箱中余油 20升时,该汽车行驶了多少千米?(5分)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
21.(2013年四川攀枝花8分)某文具店准备购进甲,乙两种铅笔,若购进甲种钢笔100支,乙种铅笔50支,需要1000元,若购进甲种钢笔50支,乙种钢笔30支,需要550元.
(1)求购进甲,乙两种钢笔每支各需多少元?
(2)若该文具店准备拿出1000元全部用来购进这两种钢笔,考虑顾客需求,要求购进甲中钢笔的数量不少于乙种钢笔数量的6倍,且不超过乙种钢笔数量的8倍,那么该文具店共有几种进货方案?
(3)若该文具店销售每支甲种钢笔可获利润2元,销售每支乙种钢笔可获利润3元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com