
如图,直线PA是一次函数 的图象,直线PB是一次函数
的图象,直线PB是一次函数 的图象.
的图象.
(1)求A、B、P三点的坐标;(2)求四边形PQOB的面积;
(1)A(-1,0),B(1,0),
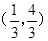 ;(2)
;(2)
解析试题分析:本题考查了一次函数综合题,难度一般,关键是掌握把四边形的面积分成两个三角形面积的差进行求解.(1)令一次函数y=x+1与一次函数y=-2x+2的y=0可分别求出A,B的坐标,再由 y=x+1和 y=?2x+2 构建二元一次方程组,可求出点P的坐标;
(2)根据四边形PQOB的面积=S△BOM-S△QPM即可求解.
试题解析:
解:(1)∵一次函数y=x+1的图象与x轴交于点A,
∴A(-1,0),
∵一次函数y=-2x+2的图象与x轴交于点B,
∴B(1,0),
∵一次函数y=x+1的图象与一次函数y=-2x+2的图象交与点P
∴ 解得:
解得:
∴点P的坐标是: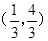
(2)∵直线PA与y轴交于点Q,则Q(0,1),设直线PB与y轴交于点M,则M(0,2),
∴

 .
.
考点:一次函数综合题.


科目:初中数学 来源: 题型:解答题
某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨1.9元收费.如果超过20吨,未超过的部分按每吨1.9元收费,超过的部分按每吨2.8元收费.设某户每月用水量为x吨,应收水费为y元.
(1)分别写出每月用水量未超过20吨和超过20吨,y与x间的函数关系式.
(2)若该城市某户5月份水费平均为每吨2.2元,求该户5月份用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
“母亲节”到了,八年级(1)班班委发起慰问烈属王大妈的活动,决定在“母亲节”期间全班同学利用课余时间去卖鲜花筹集慰问金.已知同学们从花店按每支1.2元买进鲜花,并按每支3元卖出.
(1)求同学们卖出鲜花的销售额 (元)与销售量
(元)与销售量 (支)之间的函数关系式;
(支)之间的函数关系式;
(2)若从花店购买鲜花的同时,还总共用去40元购买包装材料,求所筹集的慰问金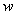 (元)与销售量
(元)与销售量 (支)之间的函数关系式;若要筹集不少于500元的慰问金,则至少要卖出鲜花多少支?(慰问金=销售额-成本)
(支)之间的函数关系式;若要筹集不少于500元的慰问金,则至少要卖出鲜花多少支?(慰问金=销售额-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,直线 +2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD.
+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD.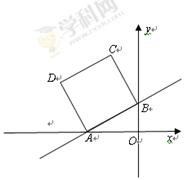
(1)求点A、B的坐标,并求边AB的长;
(2)求点D和点C的坐标;
(3)你能否在x轴上找一点M,使△MDB的周长最小?如果能,请求出M点的坐标;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
点P(x,y)在第一象限,且x+y=10,点A的坐标为(8,0),设原点为O,△OPA的面积为S.
(1)求S与x的函数关系式,写出x的取值范围,画出这个函数图象;
(2)当S=12时,求点P的坐标;
(3)△OPA的面积能大于40吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某公司专销产品 ,第一批产品
,第一批产品 上市40天内全部售完.该公司对第一批产品
上市40天内全部售完.该公司对第一批产品 上市后的市场销售情况进行了跟踪调查,调查结果如图所示,其中图1中的折线表示的是市场日销售量与上市时间的关系;图2中的折线表示的是每件产品
上市后的市场销售情况进行了跟踪调查,调查结果如图所示,其中图1中的折线表示的是市场日销售量与上市时间的关系;图2中的折线表示的是每件产品 的销售利润与上市时间的关系.
的销售利润与上市时间的关系.
(1)试写出第一批产品 的市场日销售量
的市场日销售量 与上市时间的关系式;
与上市时间的关系式;
(2)第一批产品 上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?(说明理由)
上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?(说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某工程机械厂根据市场需求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22 400万元,但不超过22 500万元,且所筹资金全部用于生产此两型挖掘机,所生产的此两型挖掘机可全部售出,此两型挖掘机的生产成本和售价如下表:
| 型号 | A | B |
| 成本(万元/台) | 200 | 240 |
| 售价(万元/台) | 250 | 300 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com