
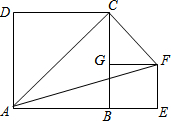
 如图,正方形ABCD的边长为a,正方形BEFG的边长为b,
如图,正方形ABCD的边长为a,正方形BEFG的边长为b,分析 (1)根据题意得到AE=a+b,EF=b,利用三角形面积计算公式即可求出答案;
(2)先补全图,利用S△ACF=S四边形AEHD-S△ADC-S△AEF-S△CHF求出答案.
解答 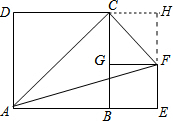 解:(1)S△AEF=$\frac{1}{2}$AE•EF=$\frac{1}{2}$(AB+BE)•EF=$\frac{1}{2}$(a+b)•b=$\frac{1}{2}$ab+$\frac{1}{2}$b2;
解:(1)S△AEF=$\frac{1}{2}$AE•EF=$\frac{1}{2}$(AB+BE)•EF=$\frac{1}{2}$(a+b)•b=$\frac{1}{2}$ab+$\frac{1}{2}$b2;
(2)作图如右:
S△ACF=S四边形AEHD-S△ADC-S△AEF-S△CHF
=a(a+b)-$\frac{1}{2}$a2-$\frac{1}{2}$ab-$\frac{1}{2}$b2-$\frac{1}{2}$b(a-b)
=$\frac{1}{2}$a2.
点评 本题主要考查了整式的混合运算的知识,解答本题的关键是熟练掌握三角形的面积计算公式,此题难度不大.


科目:初中数学 来源: 题型:解答题
 某校数学兴趣小组要测量天塔CD的高度,如图,他们在点A处测得天塔最高点C的仰角为45°,再往天塔方向前进至点B处测得最高点C的仰角为54°,AB=27m,根据这个兴趣小组测得的数据,计算天塔的高度CD(tan36°≈0.73,结果保留整数).
某校数学兴趣小组要测量天塔CD的高度,如图,他们在点A处测得天塔最高点C的仰角为45°,再往天塔方向前进至点B处测得最高点C的仰角为54°,AB=27m,根据这个兴趣小组测得的数据,计算天塔的高度CD(tan36°≈0.73,结果保留整数).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 四个村庄A、B、C、D位置如图,现要在平面内建造一个天然气供应站,并从供应站向四个村庄铺设天然气管道,为使铺设的管道总长最短,则天然气供应站应建造的位置是( )
四个村庄A、B、C、D位置如图,现要在平面内建造一个天然气供应站,并从供应站向四个村庄铺设天然气管道,为使铺设的管道总长最短,则天然气供应站应建造的位置是( )| A. | 点A处 | B. | 线段AC的中点处 | ||
| C. | 任意两村庄所连线段的中点处 | D. | 线段AC和线段BD的交点处 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
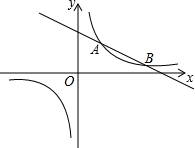 如图,一次函数,一次函数y=kx+5(k为常数,k≠0)的图象与反比例函数$y=\frac{8}{x}$的图象相交于A(2,b),B两点.
如图,一次函数,一次函数y=kx+5(k为常数,k≠0)的图象与反比例函数$y=\frac{8}{x}$的图象相交于A(2,b),B两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com