
【题目】如图,PA、PB是⊙O的切线,切点分别为A、B,直线OP交⊙O于点D、E,交AB于点C.
(1)写出图中所有的全等三角形;
(2)已知PA=4,PD=2,求⊙O的半径.
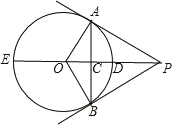
【答案】(1)△AOP≌△BOP,△AOC≌△BOC,△ACP≌△BCP;(2)⊙O的半径为3.
【解析】
(1)根据切线长定理得到PA=PB,∠OPA=∠OPB,再根据切线的性质得到∠OAP=∠OBP=90°,然后根据三角形全的判定方法易得△AOP≌△BOP,△AOC≌△BOC,△ACP≌△BCP;
(2)设⊙O的半径为r,则OA=OD=r,在Rt△OAP中根据勾股定理得到r2+42=(r+2)2,然后解方程即可.
(1)△AOP≌△BOP,△AOC≌△BOC,△ACP≌△BCP;
(2)设⊙O的半径为r,则OA=OD=r,
∵PA是⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
在Rt△OAP中,∵OA2+PA2=OP2,
∴r2+42=(r+2)2,
解得r=3,
即⊙O的半径为3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某空调厂的装配车间计划组装9000台空调.
(1)从组装空调开始,每天组装的台数m(单位:台/天)与生产时间t(单位:天)之间有怎样的函数关系?
(2)原计划用2个月时间(每月以30天计算)完成,由于气温提前升高,厂家决定这批空调提前10天上市,那么原装配车间每天至少要组装多少台空调?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.

(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的函数y=kx2+k2x﹣2的图象与y轴交于点C,
(1)当k=﹣2时,求图象与x轴的公共点个数;
(2)若图象与x轴有一个交点为A,当△AOC是等腰三角形时,求k的值.
(3)若x≥1时函数y随着x的增大而减小,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.AD与BC相交于点F,连结BE,DC,已知EF=2,CD=5,则AD=______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知∠MAN=135°,正方形ABCD绕点A旋转.
(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM,AN分别与正方形ABCD的边CB,CD的延长线交于点M,N,连接MN.
①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是 ;
②如图2,若BM≠DN,请判断①中的数量关系是否仍成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM,AN分别与直线BD交于点M,N,探究:以线段BM,MN,DN的长度为三边长的三角形是何种三角形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内气体的气压大于150kPa时,气球将爆炸.为了安全,气体体积V应该是( )

A.小于0.64m3 B.大于0.64m3 C.不小于0.64m3 D.不大于0.64m3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当m是何值时,关于x的方程(m2+2)x2+(m﹣1)x﹣4=3x2
(1)是一元二次方程;
(2)是一元一次方程;
(3)若x=﹣2是它的一个根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙O的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
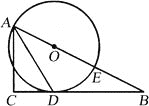
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com