
【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙O的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
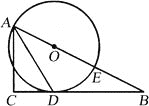
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)证明见解析(2)![]()
【解析】试题分析:(1)、连接OD,根据切线的性质以及∠C的度数得出OD∥AC,从而的得出∠CAD=∠ADO,然后根据OA=OD得出∠OAD=∠ADO,从而说明角平分线;(2)、首先根据韦达定理求出AD的长度,连接DE,根据题意得出△ACD和△ADE相似,从而得出AE的长度,然后得出圆的半径.
试题解析:(1)连接OD, ∵BC是⊙O的切线, ∴OD⊥BC ∴∠ODB=90°
又∵∠C=90° ∴AC∥OD ∴∠CAD=∠ADO 又∵OA=OD ∴∠OAD=∠ADO
∴∠CAD=∠OAD ∴ AD平分∠BAC
(2)在Rt△ACD中 AD=![]()
连接DE, ∵AE为⊙O的直径 ∴∠ADE=90° ∴∠ADE=∠C ∵∠CAD=∠OAD
∴△ACD∽△ADE ∴![]() , 即
, 即![]() ∴AE=
∴AE=![]() ∴⊙O的半径是
∴⊙O的半径是![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】根据题意解答 
(1)感知:如图①,在△ABC中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°,求∠DAE度数;
(2)探究:如图②,在△ABC中,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC,其他条件不变,求∠DFE的度数”;
(3)拓展:如图③,若把△ABC变成四边形ABEC,把AE⊥BC变成EA平分∠BEC,其他条件不变,∠DAE的度数是否变化,并且说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,已知两邻边AD=12,AB=5,P是AD边上异于A和D的任意一点,且PE⊥BD,PF⊥AC,E、F分别是垂足,那么PE+PF= . 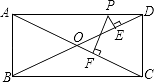
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB∥CD,AB,CD被直线l所截,点P是l上的一动点,连接PA,PC.
(1)如图①,当P在AB,CD之间时,求证:∠APC=∠A+∠C; 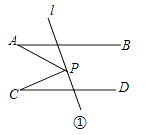
(2)如图②,当P在射线ME上时,探究∠A,∠C,∠APC的关系并证明; 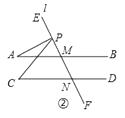
(3)如图③,当P在射线NF上时,直接写出∠A,∠C,∠APC三者之间关系. 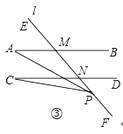
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在括号前面添上“+”或“-”或在括号内填空.
(1)-a+b=________(a-b);
(2)-m2-2m+5=-(______________);
(3)(x-y)3=________(y-x)3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com