
����Ŀ������������ 
��1����֪����ͼ�٣��ڡ�ABC�У�ADƽ�֡�BAC��AE��BC����B=40�㣬��C=70�㣬���DAE������
��2��̽������ͼ�ڣ��ڡ�ABC�У����ѡ�AE��BC����ɡ���F��DA���ӳ����ϣ�FE��BC�������������䣬���DFE�Ķ�������
��3����չ����ͼ�ۣ����ѡ�ABC����ı���ABEC����AE��BC���EAƽ�֡�BEC�������������䣬��DAE�Ķ����Ƿ�仯������˵�����ɣ�
���𰸡�
��1���⣺�ߡ�B=40�㣬��C=70�㣬
���BAC=70�㣬
��ADƽ�֡�BAC��
���BAD=��CAD=35�㣬
���ADE=��B+��BAD=75�㣬
��AE��BC��
���AEB=90�㣬
���DAE=90�㩁��ADE=15�㣮
��2���⣺ͬ��1�����ɵã���ADE=75�㣬
��FE��BC��
���FEB=90�㣬
���DFE=90�㩁��ADE=15�㣮
��3���⣺���ۣ���DAE�Ķ�����С���䣮
֤������AEƽ�֡�BEC��
���AEB=��AEC��
���C+��CAE=��B+��BAE��
�ߡ�CAE=��CAD����DAE����BAE=��BAD+��DAE��
���C+��CAD����DAE=��B+��BAD+��DAE��
��ADƽ�֡�BAC��
���BAD=��CAD��
��2��DAE=��C����B=30�㣬
���DAE=15�㣮
����������1�������ADE�Ķ��������á�DAE=90�㩁��ADE���������DAE�Ķ�������2�������ADE�Ķ��������á�DFE=90�㩁��ADE���������DAE�Ķ�������3������AEƽ�֡�BEC��ADƽ�֡�BAC�������DFE=15�㼴����õ�֤����
�����㾫����������Ĺؼ��������������ε��ڽǺ���ǵ����֪ʶ�����������ε������ڽ��У�ֻ������һ���ڽ���ֱ�ǻ�۽ǣ�ֱ�������ε�������ǻ��ࣻ�����ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��B��C�����������ϴ����������У���AC=3AB=6����BΪԭ�㣬���C����ʾ�����ǣ� ��
A. ��6B. 2C. 4D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������װ�г���ɫ����ȫ��ͬ��2�������1������
��1���ִӴ�������1�����Żأ���Ͼ��Ⱥ�������1�������û���״ͼ���б��ķ��������һ���������ڶ�����������ĸ��ʣ�
��2���ȴӴ�������1����Żأ�������1����������������������1�������1������ĸ����Ƕ��٣���ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������ÿ̨���۷ֱ�Ϊ200Ԫ��170Ԫ��A��B�����ͺŵĵ���ȣ������ǽ����ܵ����������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 5̨ | 1800Ԫ |
�ڶ��� | 4̨ | 10̨ | 3100Ԫ |
�����ۡ��ۼ۾����ֲ��䣬����=�������멁�����ɱ���
��1����A��B�����ͺŵĵ���ȵ����۵��ۣ�
��2�����������ò�����5400Ԫ�Ľ���ٲɹ��������ͺŵĵ���ȹ�30̨����A���ͺŵĵ��������ܲɹ�����̨��
��3���ڣ�2���������£�������������30̨������ܷ�ʵ������Ϊ1400Ԫ��Ŀ�ꣿ���ܣ��������Ӧ�IJɹ������������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABCΪֱ�������Σ���C=90�㣬��BC�ǡ�O�����ߣ��е�ΪD��AB����Բ��O����Բ�ཻ�ڵ�E������AD��
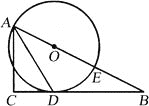
��1����֤��ADƽ�֡�BAC��
��2����AC=8��tan��DAC=![]() �����O�İ뾶��
�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ϲ����ж���ʽ��
��1��x2+5y����4x2��3y��1����
��2��3��4x2��3x+2����2��1��4x2+x��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com