
分析 把方程组进行转化为为$\left\{\begin{array}{l}{x+ay=2z}\\{x•ay=a(2{z}^{2}+3z+1)}\end{array}\right.$,把x,ay看成方程a2-2za+a(2z2+3z+1)=0的两根,利用根的判别式△≥0,根据二次函数的性质得到不等式组,求出不等式组的解集,即可解答.
解答 解:把原方程组化为$\left\{\begin{array}{l}{x+ay=2z}\\{x•ay=a(2{z}^{2}+3z+1)}\end{array}\right.$,
把x,ay看方程a2-2za+a(2z2+3z+1)=0的两根,
∵x,ay都是实根,
∴△=4z2-4a(2z2+3z+1)≥0,
z2-2az2-3az-a≥0,
(1-2a)z2-3az-a≥0
根据二次函数的性质,可得:$\left\{\begin{array}{l}{1-2a>0}\\{9{a}^{2}+4a(1-2a)<0}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a<\frac{1}{2}}\\{-4<a<0}\end{array}\right.$,
∴-4<a<0.
点评 本题考查了二元一次方程组的解、一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根,解集本题的关键是利用根的判别式得到不等式组.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
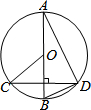 如图所示,AB为⊙O的直径,CD为弦,AB⊥CD,如果∠BOC=50°,那么∠ABD的度数为( )
如图所示,AB为⊙O的直径,CD为弦,AB⊥CD,如果∠BOC=50°,那么∠ABD的度数为( )| A. | 25° | B. | 20° | C. | 65° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com