
【题目】如图,在△ABC 中,∠C=90°,BC=3,D,E分别在AB、AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )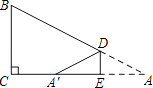
A.![]()
B.3
C.2
D.1
科目:初中数学 来源: 题型:
【题目】D,E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB,AC的中点.O是△ABC所在平面上的动点,连接OB,OC,点G,F分别是OB,OC的中点,顺次连接点D,G,F,E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;
(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣4与x轴交于A(4,0)、B(﹣2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.
(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BDBC;
(3)当△PCD的面积最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备组织七年级学生参加夏令营,已知:用3辆小客车和1辆大客车每次可运送学生105人;用一辆小客车和2辆大客车每次可运送学生110人,现有学生400人,计划租用小客车a辆,大客车b辆,一次送完,且恰好每辆车都坐满.
(1)1辆小客车和1辆大客车都坐满后一次可送多少名学生?
(2)请你帮学校设计出所有的租车方案;
(3)若小客车每辆需租金200元,大客车每辆需租金380元,请选出最省钱的方案,并求出最省租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+4(k≠0)与x轴、y轴分别交于点B,A,直线y=-2x+1与y轴交于点C,与直线y=kx+4交于点D,△ACD的面积是![]() .
.
(1)求直线AB的表达式;
(2)设点E在直线AB上,当△ACE是直角三角形时,请直接写出点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.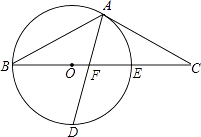
(1)求证:AC是⊙O的切线;
(2)已知圆的半径R=5,EF=3,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com