
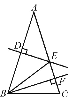
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,连接BE,求∠A的度数.
【答案】36°
【解析】
试题设∠A==x,根据线段垂直平分线的性质可得∠A=∠ABE=x,∠BEC=∠C,由三角形的外角的性质可得∠BEC=∠A+∠ABE=2x,又因△ABC是等腰三角形可得∠ABC=∠C=2x,在△ABC中,根据三角形的内角和定理列方程即可求得x.
试题解析:解:连接BE,
∵DE是线段AB的垂直平分线,
∴AE=BE
∴∠A=∠ABE,
设∠A=∠ABE=x,
∴∠BEC=∠A+∠ABE=2x,
∵CE的垂直平分线正好经过点B,与AC相交于点可知△BCE是等腰三角形,
∴∠BEC=∠C=2x,
∵△ABC是等腰三角形,
∴∠ABC=∠C=2x,
在△ABC中,∠ABC+∠C+∠A=180°,即2x+2x+x=180°,解得x=36°,
∴∠A=36°.


 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠C=90°,BC=3,D,E分别在AB、AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )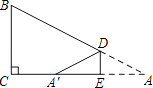
A.![]()
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,左右两幅图案关于y轴对称,右图案中的左右眼睛的坐标分别是(2,3),(4,3),嘴角左右端点的坐标分别是(2,1),(4,1).
(1)试确定左图案中的左右眼睛和嘴角左右端点的坐标;
(2)从对称的角度来考虑,说一说你是怎样得到的.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店甲、乙两种商品三天销售情况的账目记录如下表:
日期 | 卖出甲商品的数量(个) | 卖出乙商品的数量(个) | 收入(元) |
第一天 | 39 | 21 | 321 |
第二天 | 26 | 14 | 204 |
第三天 | 39 | 25 | 345 |
(1)财务主管在核查时发现:第一天的账目正确,但其他两天的账目有一天有误,请你判断第几天的账目有误,并说明理由;
(2)求甲、乙两种商品的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,ABCD中,点E,F在直线AC上(点E在F左侧),BE∥DF.

(1)求证:四边形BEDF是平行四边形;
(2)若AB⊥AC,AB=4,BC=![]() ,当四边形BEDF为矩形时,求线段AE的长.
,当四边形BEDF为矩形时,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱底面半径为![]() cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A. 12cm B. ![]() cm C. 15cm D.
cm C. 15cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,点E、F分别是AD、AB的中点,EF交AC于点G,那么AG:GC的值为( )
A.1:2
B.1:3
C.1:4
D.2:3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com