
【题目】如图,直线y=kx+4(k≠0)与x轴、y轴分别交于点B,A,直线y=-2x+1与y轴交于点C,与直线y=kx+4交于点D,△ACD的面积是![]() .
.
(1)求直线AB的表达式;
(2)设点E在直线AB上,当△ACE是直角三角形时,请直接写出点E的坐标.

【答案】(1)直线AB的表达式为y=x+4;(2)当△ACE是直角三角形时,点E的坐标为(-3,1)或(-![]() ,
,![]() ).
).
【解析】
(1)将=0分别代入两个一次函数表达式中求出点A、C的坐标,进而即可得出AC的长度,再根据三角形的面积公式结合△ACD的面积即可求出点D的横坐标,利用一次函数图象上点的坐标特即可求出点D的坐标,由点D的坐标利用待定系数法即可求出直线AB的表达式;
(2)由直线AB的表达式即可得出△ACE为等腰直角三角形,分∠ACE=90![]() 和∠AEC=90
和∠AEC=90![]() 两种情况考虑,根据点A、C的坐标利用等腰直角三角形的性质即可得出点E的坐标,此题得解.
两种情况考虑,根据点A、C的坐标利用等腰直角三角形的性质即可得出点E的坐标,此题得解.
(1)当x=0时,y=kx+4=4,y=-2x+1=1,
∴A(0,4),C(0,1),
∴AC=3.
∵S△ACD=![]() AC·(-xD)=-
AC·(-xD)=-![]() xD=
xD=![]() ,
,
∴xD=-1.
当x=-1时,y=-2x+1=3,
∴D(-1,3).
将D(-1,3)代入y=kx+4,得-k+4=3,
解得k=1,
∴直线AB的表达式为y=x+4.
(2)∵直线AB的表达式为y=x+4,
∴△ACE为等腰直角三角形.
如图,当∠ACE=90°时,
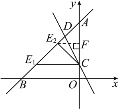
∵A(0,4),C(0,1),AC=3,
∴CE1=3,E1的横坐标为-3.
将x=-3代入y=x+4中,得y=1,
∴E1(-3,1);
当∠AE2C=90°时,
∵A(0,4),C(0,1),AC=3,
过点E2作E2F⊥AC于点F,E2F=AF=FC=![]() AC=
AC=![]() ,
,
∴E2(-![]() ,
,![]() ).
).
综上所述,当△ACE是直角三角形时,点E的坐标为(-3,1)或(-![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】某手机经销商计划同时购进一批甲、乙两种型号的手机,若购进2台甲型号手机和1台乙型号手机,共需要资金2800元;若购进3台甲型号手机和2台乙型号手机,共需要资金4600元.
(1)求甲、乙型号手机每台进价为多少元?
(2)该店计划购进甲、乙两种型号的手机销售,预计用不多于1.8万元且不少于1.74万元的资金购进这两种手机共20台,请问有几种进货方案?请写出进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请在图中标明旋转中心P的位置并写出其坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠C=90°,BC=3,D,E分别在AB、AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )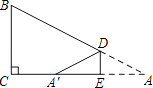
A.![]()
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一等腰直角三角形纸片,以它的对称轴为折痕,将三角形对折,得到的三角形还是等腰直角三角形(如图).依照上述方法将原等腰直角三角形折叠四次,所得小等腰直角三角形的周长是原等腰直角三角形周长的倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“2016年联欢会”中,有一个摸奖游戏:有4张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,2张是哭脸,现将4张纸牌洗匀后背面朝上摆放到桌上,然后让同学去翻纸牌.
(1)现在小芳和小霞分别有一次翻牌机会,若正面是笑脸,则小芳获奖;若正面是哭脸,则小霞获奖,她们获奖的机会相同吗?判断并说明理由.
(2)如果小芳、小明都有翻两张牌的机会.翻牌规则:小芳先翻一张,放回后再翻一张;小明同时翻开两张纸牌.他们翻开的两张纸牌中只要出现笑脸就获奖.请问他们获奖的机会相等吗?判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线![]() ,点
,点![]() 为平面上一点,连接
为平面上一点,连接![]() 与
与![]() .
.
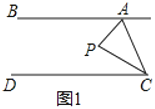
(1)如图1,点![]() 在直线
在直线![]() 、
、![]() 之间,当
之间,当![]() ,
,![]() 时,求
时,求![]() .
.
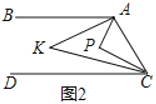
(2)如图2,点![]() 在直线
在直线![]() 、
、![]() 之间
之间![]() 左侧,
左侧,![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,写出
,写出![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
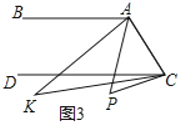
(3)如图3,点![]() 落在
落在![]() 下方,
下方,![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,
,![]() 与
与![]() 有何数量关系?并说明理由.
有何数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,左右两幅图案关于y轴对称,右图案中的左右眼睛的坐标分别是(2,3),(4,3),嘴角左右端点的坐标分别是(2,1),(4,1).
(1)试确定左图案中的左右眼睛和嘴角左右端点的坐标;
(2)从对称的角度来考虑,说一说你是怎样得到的.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,ABCD中,点E,F在直线AC上(点E在F左侧),BE∥DF.

(1)求证:四边形BEDF是平行四边形;
(2)若AB⊥AC,AB=4,BC=![]() ,当四边形BEDF为矩形时,求线段AE的长.
,当四边形BEDF为矩形时,求线段AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com