
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请在图中标明旋转中心P的位置并写出其坐标.
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好.
(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2 , 并指出她与嘉嘉抽到勾股数的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个角之差的绝对值等于60°,则称这两个角互为“互优角”,(本题中所有角都是指大于0°且小于180°的角).
(1)若∠1和∠2互为“互优角”,当∠1=90°时,则∠2=_____°;
(2)如图1,将一长方形纸片沿着EP对折(点P在线段BC上,点E在线段AB上)使点B落在点若与互为“互优角”,求∠BPE的度数;
(3)再将纸片沿着PF对折(点F在线段CD或AD上)使点C落在C′:
①如图2,若点E、C′、P在同一直线上,且![]() 与
与![]() 互为“互优角”,求∠EPF的度数(对折时,线段落在∠EPF内部);
互为“互优角”,求∠EPF的度数(对折时,线段落在∠EPF内部);
②若∠B′PC′与∠EPF互为“互优角”,则∠BPE求∠CPF应满足什么样的数量关系(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】D,E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB,AC的中点.O是△ABC所在平面上的动点,连接OB,OC,点G,F分别是OB,OC的中点,顺次连接点D,G,F,E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线AB∥CD,E为AB、CD间的一点,连接EA、EC.
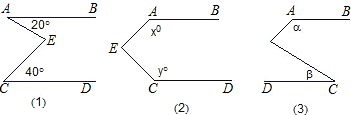
(1)如图①,若∠A=20°,∠C=40°,则∠AEC= °.
(2)如图②,若∠A=x°,∠C=y°,则∠AEC= °.
(3)如图③,若∠A=α,∠C=β,则α,β与∠AEC之间有何等量关系.并简要说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;
(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣4与x轴交于A(4,0)、B(﹣2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.
(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BDBC;
(3)当△PCD的面积最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+4(k≠0)与x轴、y轴分别交于点B,A,直线y=-2x+1与y轴交于点C,与直线y=kx+4交于点D,△ACD的面积是![]() .
.
(1)求直线AB的表达式;
(2)设点E在直线AB上,当△ACE是直角三角形时,请直接写出点E的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com