
ЁОЬтФПЁПШчЙћСНИіНЧжЎВюЕФОјЖджЕЕШгк60ЁуЃЌдђГЦетСНИіНЧЛЅЮЊЁАЛЅгХНЧЁБЃЌ(БОЬтжаЫљгаНЧЖМЪЧжИДѓгк0ЁуЧваЁгк180ЁуЕФНЧ)ЃЎ
(1)ШєЁЯ1КЭЁЯ2ЛЅЮЊЁАЛЅгХНЧЁБЃЌЕБЁЯ1=90ЁуЪБЃЌдђЁЯ2=_____ЁуЃЛ
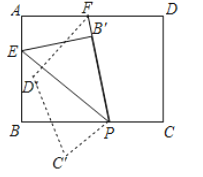
(2)ШчЭМ1ЃЌНЋвЛГЄЗНаЮжНЦЌбизХEPЖдел(ЕуPдкЯпЖЮBCЩЯЃЌЕуEдкЯпЖЮABЩЯ)ЪЙЕуBТфдкЕуШєгыЛЅЮЊЁАЛЅгХНЧЁБЃЌЧѓЁЯBPEЕФЖШЪ§ЃЛ
(3)дйНЋжНЦЌбизХPFЖдел(ЕуFдкЯпЖЮCDЛђADЩЯ)ЪЙЕуCТфдкCЁфЃК
ЂйШчЭМ2ЃЌШєЕуEЁЂCЁфЁЂPдкЭЌвЛжБЯпЩЯЃЌЧв![]() гы
гы![]() ЛЅЮЊЁАЛЅгХНЧЁБЃЌЧѓЁЯEPFЕФЖШЪ§(ЖделЪБЃЌЯпЖЮТфдкЁЯEPFФкВП)ЃЛ
ЛЅЮЊЁАЛЅгХНЧЁБЃЌЧѓЁЯEPFЕФЖШЪ§(ЖделЪБЃЌЯпЖЮТфдкЁЯEPFФкВП)ЃЛ
ЂкШєЁЯBЁфPCЁфгыЁЯEPFЛЅЮЊЁАЛЅгХНЧЁБЃЌдђЁЯBPEЧѓЁЯCPFгІТњзуЪВУДбљЕФЪ§СПЙиЯЕ(жБНгаДГіНсЙћМДПЩ)ЃЎ

ЁОД№АИЁПЃЈ1ЃЉ30ЁуЛђ150ЃЛЃЈ2ЃЉ40ЁуЛђ80ЁуЃЛЃЈ3ЃЉЂйЁЯEPF=80ЁуЃЌЂкЁЯEPF=40ЁуЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉАДееЁАЛЅгХНЧЕФЖЈвхЃЌЧѓГіЁЯ2МДПЩЃЛ
ЃЈ2ЃЉИљОнЁЯEPB'+ЁЯEPB'+ЁЯEPB'+60Ёу=180ЁуНтД№МДПЩЃЛ
ЃЈ3ЃЉЂйгЩЁЯBPE+ЁЯEPB'+ЁЯB'PF+ЁЯFPC=180ЁуНтД№МДПЩЃЛ
ЂкЁЯB'PC'=ЁЯFPCЃЌЁЯEPB=ЁЯEPFЃЌЁЯEPB+ЁЯEPF+ЁЯFPC=180ЁуНтД№МДПЩЃЎ
НтЃКЃЈ1ЃЉЁпЁЯ1КЭЁЯ2ЛЅЮЊЁАЛЅгХНЧ
Ёр|ЁЯ1-ЁЯ2|=60Ёу
ЁпЁЯ1ЃН90Ёу
Ёр90Ёу-ЁЯ2=60ЁуЛђ90Ёу-ЁЯ2=-60Ёу
НтЕУЃКЁЯ2=30ЁуЛђ150Ёу
ЙЪД№АИЮЊЃК30ЁуЛђ150ЃЎ
ЃЈ2ЃЉЁпЁЯEPB'гыЁЯB'PCЛЅЮЊЁАЛЅгХНЧЁБ
ЕБЁЯEPB'<ЁЯB'PCЪБЃЌЁЯB'PC-ЁЯEPB'=60Ёу
ЁрЁЯB'PC=ЁЯEPB'+60Ёу
ЁпЁїBEPЗелЕУЁїB'EP
ЁрЁЯEPB=ЁЯEPB'
ЁпЁЯEPB+ЁЯEPB'+ЁЯB'PC=180Ёу
ЁрЁЯEPB'+ЁЯEPB'+ЁЯEPB'+60Ёу=180
НтЕУЃКЁЯEPB'=40Ёу
ЕБЁЯEPB'>ЁЯB'PCЪБЃЌЁЯB'PC-ЁЯEPB'=60ЁуЃЌПЩЕУЁЯEPB'=80Ёу
ЙЪЁЯEPB'ЕФжЕЮЊ40ЁуЛђ80ЁуЃЛ
ЃЈ3ЃЉЂйгЩЬтвтЕУЃКЕуEЁЂCЁЂPдкЭЌвЛжБЯпЩЯЃЌ
ЁпЁЯB'PC'гыЁЯEPFЛЅЮЊЁАЛЅгХНЧ
ЁрЁЯBPC<ЁЯEPFЃЌЁЯEPF-ЁЯB'PC=60Ёу=ЁЯB'PF
ЁпЁЯBPE=ЁЯB'PC=ЁЯEPF-60ЁуЃЌЁЯFPC=ЁЯEPF
ЁрЁЯBPE+ЁЯEPB'+ЁЯB'PF+ЁЯFPC=180Ёу
ЁрЁЯEPF-60Ёу+ЁЯEPF+ЁЯEPF=180ЁуЃЌЕУЁЯEPF=80ЁуЃЛ
ЂкгЩЬтвтЕУЃКЕуEЁЂCЁЂPдкЭЌвЛжБЯпЩЯЃЌ
ЁпЁЯB'PC'гыЁЯEPFЛЅЮЊЁАЛЅгХНЧ
ЁрЁЯB'P'C-ЁЯEPF=60ЁуЃЌЕУЁЯB'P'C=60Ёу+ЁЯEPF
ЁпЁЯB'PC'=ЁЯFPCЃЌЁЯEPB=ЁЯEPFЃЌЁЯEPB+ЁЯEPF+ЁЯFPC=180Ёу
Ёр2ЁЯEPF+60Ёу+ЁЯEPF=180ЁуЃЌНтЕУЁЯEPF=40ЁуЃЎ
ЙЪЁЯEPFЕФЖШЪ§ЮЊ40ЁуЃЎ


 бєЙтПЮЬУПЮЪБгХЛЏзївЕЯЕСаД№АИ
бєЙтПЮЬУПЮЪБгХЛЏзївЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯAЃН48ЁуЃЌЁЯABCгыЁЯACDЕФЦНЗжЯпНЛгкЕуA1ЃЌЕУЁЯA1ЃЛЁЯA1BCгыЁЯA1CDЕФЦНЗжЯпЯрНЛгкЕуA2ЃЌЕУЁЯA2ЃЛЁЁЃЛЁЯAnЃ1BCгыЁЯAnЃ1CDЕФЦНЗжЯпНЛгкЕуAnЃЌвЊЪЙЁЯAnЕФЖШЪ§ЮЊећЪ§ЃЌдђnЕФзюДѓжЕЮЊ(ЁЁЁЁ)
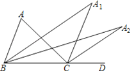
A.2B.3C.4D.5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпy=Љ ![]() x+2
x+2 ![]() гыxжсЃЌyжсЗжБ№НЛгкЕуAЃЌЕуBЃЌСНЖЏЕуDЃЌEЗжБ№ДгЕуAЃЌЕуBЭЌЪБГіЗЂЯђЕуOдЫЖЏЃЈдЫЖЏЕНЕуOЭЃжЙЃЉЃЌдЫЖЏЫйЖШЗжБ№ЪЧ1ИіЕЅЮЛГЄЖШ/УыКЭ
гыxжсЃЌyжсЗжБ№НЛгкЕуAЃЌЕуBЃЌСНЖЏЕуDЃЌEЗжБ№ДгЕуAЃЌЕуBЭЌЪБГіЗЂЯђЕуOдЫЖЏЃЈдЫЖЏЕНЕуOЭЃжЙЃЉЃЌдЫЖЏЫйЖШЗжБ№ЪЧ1ИіЕЅЮЛГЄЖШ/УыКЭ ![]() ИіЕЅЮЛГЄЖШ/УыЃЌЩшдЫЖЏЪБМфЮЊtУыЃЌвдЕуAЮЊЖЅЕуЕФХзЮяЯпОЙ§ЕуEЃЌЙ§ЕуEзїxжсЕФЦНааЯпЃЌгыХзЮяЯпЕФСэвЛИіНЛЕуЮЊЕуGЃЌгыABЯрНЛгкЕуFЃЎ
ИіЕЅЮЛГЄЖШ/УыЃЌЩшдЫЖЏЪБМфЮЊtУыЃЌвдЕуAЮЊЖЅЕуЕФХзЮяЯпОЙ§ЕуEЃЌЙ§ЕуEзїxжсЕФЦНааЯпЃЌгыХзЮяЯпЕФСэвЛИіНЛЕуЮЊЕуGЃЌгыABЯрНЛгкЕуFЃЎ
ЃЈ1ЃЉЧѓЕуAЃЌЕуBЕФзјБъЃЛ
ЃЈ2ЃЉгУКЌtЕФДњЪ§ЪНЗжБ№БэЪОEFКЭAFЕФГЄЃЛ
ЃЈ3ЃЉЕБЫФБпаЮADEFЮЊСтаЮЪБЃЌЪдХаЖЯЁїAFGгыЁїAGBЪЧЗёЯрЫЦЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ4ЃЉЪЧЗёДцдкtЕФжЕЃЌЪЙЁїAGFЮЊжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіетЪБХзЮяЯпЕФНтЮіЪНЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪжЛњОЯњЩЬМЦЛЎЭЌЪБЙКНјвЛХњМзЁЂввСНжжаЭКХЕФЪжЛњЃЌШєЙКНј2ЬЈМзаЭКХЪжЛњКЭ1ЬЈвваЭКХЪжЛњЃЌЙВашвЊзЪН№2800дЊЃЛШєЙКНј3ЬЈМзаЭКХЪжЛњКЭ2ЬЈвваЭКХЪжЛњЃЌЙВашвЊзЪН№4600дЊЃЎ
ЃЈ1ЃЉЧѓМзЁЂвваЭКХЪжЛњУПЬЈНјМлЮЊЖрЩйдЊЃП
ЃЈ2ЃЉИУЕъМЦЛЎЙКНјМзЁЂввСНжжаЭКХЕФЪжЛњЯњЪлЃЌдЄМЦгУВЛЖргк1ЃЎ8ЭђдЊЧвВЛЩйгк1ЃЎ74ЭђдЊЕФзЪН№ЙКНјетСНжжЪжЛњЙВ20ЬЈЃЌЧыЮЪгаМИжжНјЛѕЗНАИЃПЧыаДГіНјЛѕЗНАИЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЪ§жсЩЯЃЌЕуMЁЂNЗжБ№БэЪОЪ§mЃЌnЃЎ дђЕуMЃЌN жЎМфЕФОрРыЮЊ|m-n|ЃЎвбжЊЕуAЃЌBЃЌCЃЌDдкЪ§жсЩЯЗжБ№БэЪОЕФЪ§ЮЊaЃЌbЃЌcЃЌdЃЎЧв|a-c|=|b-c|=![]() |d-a|=1 (aЁйb)ЃЌдђЯпЖЮBDЕФГЄЖШЮЊЃЈ ЃЉ
|d-a|=1 (aЁйb)ЃЌдђЯпЖЮBDЕФГЄЖШЮЊЃЈ ЃЉ
A.3.5B.0.5C.3.5Лђ0.5D.4.5Лђ0.5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЬхг§ЩчЭХдкаЃФкПЊеЙЁАФузюЯВЛЖЕФЬхг§ЯюФПЪЧЪВУДЃП![]() ЫФЯюбЁвЛЯю
ЫФЯюбЁвЛЯю![]() ЁБЕїВщЃЌЖдОХФъМЖбЇЩњЫцЛњГщбљЃЌВЂНЋЪеМЏЕФЪ§ОнЛцжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎЧыНсКЯЭГМЦЭМЃЌНтД№ЯТСаЮЪЬтЃК
ЁБЕїВщЃЌЖдОХФъМЖбЇЩњЫцЛњГщбљЃЌВЂНЋЪеМЏЕФЪ§ОнЛцжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎЧыНсКЯЭГМЦЭМЃЌНтД№ЯТСаЮЪЬтЃК

(1)БОДЮГщбљШЫЪ§га________ШЫЃЛ
(2)ВЙШЋЬѕаЮЭГМЦЭМКЭЩШаЮЭГМЦЭМЃЛ
(3)ИУаЃОХФъМЖЙВга600УћбЇЩњЃЌЙРМЦОХФъМЖзюЯВЛЖЬјЩўЯюФПЕФбЇЩњга________ШЫЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЖдЁАбЇЩњдкбЇаЃФУЪжЛњгАЯьбЇЯАЕФЧщПіЁБНјааСЫЕїВщЃЌЫцЛњЕїВщСЫВПЗжбЇЩњЃЌЖдДЫЮЪЬтЕФПДЗЈЗжЮЊШ§жжЧщПіЃКУЛгагАЯьЁЂгАЯьВЛДѓЁЂгАЯьКмДѓЃЌВЂНЋЕїВщНсЙћЛцжЦГЩШчЯТВЛЭъећЕФЭГМЦБэКЭЩШаЮЭГМЦЭМЃЌИљОнЭГМЦЭМБэЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ШЫЪ§ЭГМЦБэШчЯТЃК
ПДЗЈ | УЛгагАЯь | гАЯьВЛДѓ | гАЯьКмДѓ |
бЇЩњШЫЪ§(ШЫ) | 20 | 30 | a |
ЃЈ1ЃЉЭГМЦБэжаЕФaЃНЁЁЁЁЁЁЁЁЃЛ
ЃЈ2ЃЉЧыИљОнБэжаЕФЪ§ОнЃЌЬИЬИФуЕФПДЗЈЃЈВЛЩйгк2ЬѕЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌRtЁїABCЕФШ§ИіЖЅЕуЗжБ№ЪЧAЃЈЉ3ЃЌ2ЃЉЃЌBЃЈ0ЃЌ4ЃЉЃЌCЃЈ0ЃЌ2ЃЉЃЎ
ЃЈ1ЃЉНЋЁїABCвдЕуCЮЊа§зЊжааФа§зЊ180ЁуЃЌЛГіа§зЊКѓЖдгІЕФЁїA1B1CЃЛЦНвЦЁїABCЃЌШєЕуAЕФЖдгІЕуA2ЕФзјБъЮЊЃЈ0ЃЌЉ4ЃЉЃЌЛГіЦНвЦКѓЖдгІЕФЁїA2B2C2ЃЛ
ЃЈ2ЃЉШєНЋЁїA1B1CШЦФГвЛЕуа§зЊПЩвдЕУЕНЁїA2B2C2ЃЛЧыдкЭМжаБъУїа§зЊжааФPЕФЮЛжУВЂаДГіЦфзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌжБЯп![]() ЃЌЕу
ЃЌЕу![]() ЮЊЦНУцЩЯвЛЕуЃЌСЌНг
ЮЊЦНУцЩЯвЛЕуЃЌСЌНг![]() гы
гы![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕу![]() дкжБЯп
дкжБЯп![]() ЁЂ
ЁЂ![]() жЎМфЃЌЕБ
жЎМфЃЌЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЃЎ
ЃЎ
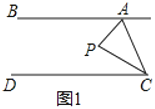
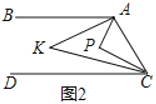
ЃЈ2ЃЉШчЭМ2ЃЌЕу![]() дкжБЯп
дкжБЯп![]() ЁЂ
ЁЂ![]() жЎМф
жЎМф![]() зѓВрЃЌ
зѓВрЃЌ![]() гы
гы![]() ЕФНЧЦНЗжЯпЯрНЛгкЕу
ЕФНЧЦНЗжЯпЯрНЛгкЕу![]() ЃЌаДГі
ЃЌаДГі![]() гы
гы![]() жЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
жЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
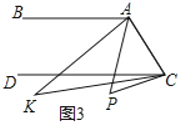
ЃЈ3ЃЉШчЭМ3ЃЌЕу![]() Тфдк
Тфдк![]() ЯТЗНЃЌ
ЯТЗНЃЌ![]() гы
гы![]() ЕФНЧЦНЗжЯпЯрНЛгкЕу
ЕФНЧЦНЗжЯпЯрНЛгкЕу![]() ЃЌ
ЃЌ![]() гы
гы![]() гаКЮЪ§СПЙиЯЕЃПВЂЫЕУїРэгЩЃЎ
гаКЮЪ§СПЙиЯЕЃПВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com