
【题目】如图,在△ABC中,∠A=48°,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;……;∠An-1BC与∠An-1CD的平分线交于点An,要使∠An的度数为整数,则n的最大值为( )
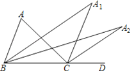
A.2B.3C.4D.5
【答案】C
【解析】
由三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠ABC+∠A,∠A1CD=∠A1BC+∠A1,根据角平分线的定义可得∠A1BC=![]() ∠ABC,∠A1CD=
∠ABC,∠A1CD=![]() ∠ACD,然后整理得到∠A1=
∠ACD,然后整理得到∠A1=![]() ∠A,根据A1B、A1C分别平分∠ABC、∠ACD可得:∠ABC=2∠A1BC,∠ACD=2∠A1CD,而∠ACD=∠A+∠ABC ,∠A1CD=∠A1+∠A1BC,于是有∠A=2∠A1,同理可得∠A1=2∠A2,继而∠A2=
∠A,根据A1B、A1C分别平分∠ABC、∠ACD可得:∠ABC=2∠A1BC,∠ACD=2∠A1CD,而∠ACD=∠A+∠ABC ,∠A1CD=∠A1+∠A1BC,于是有∠A=2∠A1,同理可得∠A1=2∠A2,继而∠A2=![]() ∠A,因此发现规律,将∠A代入即可求出使∠An的度数为整数,则n的最大值.
∠A,因此发现规律,将∠A代入即可求出使∠An的度数为整数,则n的最大值.
由三角形的外角性质可得:∠ACD=∠ABC+∠A,∠A1CD=∠A1BC+∠A1,
∵∠ABC与∠ACD的平分线交于点A1,
∴∠A1BC=![]() ∠ABC,∠A1CD=
∠ABC,∠A1CD=![]() ∠ACD,
∠ACD,
∴∠A1+∠A1BC=∠A1CD =![]() (∠ABC+∠A)=
(∠ABC+∠A)=![]() ∠A+∠A1BC,
∠A+∠A1BC,
∴∠A1=![]() ∠A=
∠A=![]() ×48°=24°,
×48°=24°,
∵A1B、A1C分别平分∠ABC、∠ACD,
∴∠ABC=2∠A1BC,∠ACD=2∠A1CD,
而∠ACD=∠A+∠ABC ,∠A1CD=∠A1+∠A1BC,
∴∠A=2∠A1,
∴∠A1=![]() ∠A,
∠A,
同理可得:∠A1=2∠A2,
∴∠A2=![]() ∠A,
∠A,
∴∠A=2n∠An,
∴∠An=![]() ∠A
∠A
∵∠A=48°
∴当n=4时,∠A4=![]() ×48°=3°,此时n的值最大,
×48°=3°,此时n的值最大,
故选:C


科目:初中数学 来源: 题型:
【题目】将△ABC绕点B逆时针旋转到△A′BC′,使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为cm2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图甲,AB∥CD,试问∠2与∠1+∠3的关系是什么,为什么?
(2)如图乙,AB∥CD,试问∠2+∠4与∠1+∠3+∠5一样大吗?为什么?
(3)如图丙,AB∥CD,试问∠2+∠4+∠6与∠1+∠3+∠5+∠7哪个大?为什么?
你能将它们推广到一般情况吗?请写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).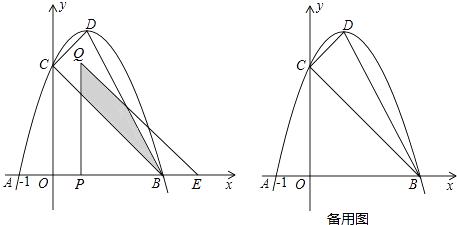
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△A'B'C',点C的对应点是直线上的格点C'.
(1)画出△A'B'C';
(2)在BC上找一点P,使AP平分△ABC的面积;
(3)试在直线l上画出所有的格点Q,使得由点A'、B'、C'、Q四点围成的四边形的面积为9.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好.
(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2 , 并指出她与嘉嘉抽到勾股数的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个角之差的绝对值等于60°,则称这两个角互为“互优角”,(本题中所有角都是指大于0°且小于180°的角).
(1)若∠1和∠2互为“互优角”,当∠1=90°时,则∠2=_____°;
(2)如图1,将一长方形纸片沿着EP对折(点P在线段BC上,点E在线段AB上)使点B落在点若与互为“互优角”,求∠BPE的度数;
(3)再将纸片沿着PF对折(点F在线段CD或AD上)使点C落在C′:
①如图2,若点E、C′、P在同一直线上,且![]() 与
与![]() 互为“互优角”,求∠EPF的度数(对折时,线段落在∠EPF内部);
互为“互优角”,求∠EPF的度数(对折时,线段落在∠EPF内部);
②若∠B′PC′与∠EPF互为“互优角”,则∠BPE求∠CPF应满足什么样的数量关系(直接写出结果即可).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com