
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好.
(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2 , 并指出她与嘉嘉抽到勾股数的可能性一样吗?
【答案】
(1)解:嘉嘉随机抽取一张卡片共出现4种等可能结果,其中抽到的卡片上的数是勾股数的结果有3种,
所以嘉嘉抽取一张卡片上的数是勾股数的概率P1= ![]() ;
;
(2)解:列表法:
A | B | C | D | |
A | (A,B) | (A,C) | (A,D) | |
B | (B,A) | (B,C) | (B,D) | |
C | (C,A) | (C,B) | (C,D) | |
D | (D,A) | (D,B) | (D,C) |
由列表可知,两次抽取卡片的所有可能出现的结果有12种,
其中抽到的两张卡片上的数都是勾股数的有6种,
∴P2= ![]() =
= ![]() ,
,
∵P1= ![]() ,P2=
,P2= ![]() ,P1≠P2
,P1≠P2
∴淇淇与嘉嘉抽到勾股数的可能性不一样.
【解析】
首先利用列表法列出所有的可能性,然后找出与嘉嘉抽到的勾股数的可能性,最后利用概率公式进行解答即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图:已知![]() .
.

(1)读句画图:画![]() 的角平分线
的角平分线![]() 、
、![]() 交
交![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() 、
、![]() 交于点
交于点![]() ,过
,过![]() 点作
点作![]() 交
交![]() 的延长线于
的延长线于![]() .
.
(2)在(1)的条件下解决下面问题:
①填表
|
|
|
|
| __________ | ______________ | ______________ |
②根据图中的数据,你发现无论![]() 是什么角,
是什么角,![]() 总是__________(填锐角、钝角或直角).
总是__________(填锐角、钝角或直角).
③若过![]() 点作
点作![]() 于
于![]() ,你能猜想
,你能猜想![]() 与
与![]() 之间的数量关系吗?说明理由.(在(1)中的图上作
之间的数量关系吗?说明理由.(在(1)中的图上作![]() 于
于![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=48°,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;……;∠An-1BC与∠An-1CD的平分线交于点An,要使∠An的度数为整数,则n的最大值为( )
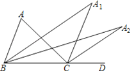
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交BC于点F.


(1)如图①,当AE⊥BC时,写出图中所有与∠B相等的角: ;所有与∠C相等的角: .
(2)若∠C-∠B=50°,∠BAD=x°(0<x≤45) .
① 求∠B的度数;
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一个均匀的转盘被平均分成六等份,分别标有![]() 这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字(当指针恰好指在分界线上时,不记,重转).
这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字(当指针恰好指在分界线上时,不记,重转).
(1)转动转盘,转出的数字大于![]() 的概率是多少;
的概率是多少;
(2)现有两张分别写有![]() 和
和![]() 的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
①这三条线段能构成三角形的概率是多少?
②这三条线段能构成等腰三角形的概率是多少?(注:要求写出各种可能情况)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 边上的中线,过点
边上的中线,过点![]() 作
作![]() 垂足为
垂足为![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)探索线段![]() 和
和![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(3)当![]() 等于多少度时,点
等于多少度时,点![]() 恰好为
恰好为![]() 中点?
中点?
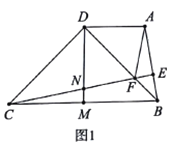
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣ ![]() x+2
x+2 ![]() 与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和
与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和 ![]() 个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
(1)求点A,点B的坐标;
(2)用含t的代数式分别表示EF和AF的长;
(3)当四边形ADEF为菱形时,试判断△AFG与△AGB是否相似,并说明理由.
(4)是否存在t的值,使△AGF为直角三角形?若存在,求出这时抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机经销商计划同时购进一批甲、乙两种型号的手机,若购进2台甲型号手机和1台乙型号手机,共需要资金2800元;若购进3台甲型号手机和2台乙型号手机,共需要资金4600元.
(1)求甲、乙型号手机每台进价为多少元?
(2)该店计划购进甲、乙两种型号的手机销售,预计用不多于1.8万元且不少于1.74万元的资金购进这两种手机共20台,请问有几种进货方案?请写出进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请在图中标明旋转中心P的位置并写出其坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com