
【题目】如图:已知![]() .
.

(1)读句画图:画![]() 的角平分线
的角平分线![]() 、
、![]() 交
交![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() 、
、![]() 交于点
交于点![]() ,过
,过![]() 点作
点作![]() 交
交![]() 的延长线于
的延长线于![]() .
.
(2)在(1)的条件下解决下面问题:
①填表
|
|
|
|
| __________ | ______________ | ______________ |
②根据图中的数据,你发现无论![]() 是什么角,
是什么角,![]() 总是__________(填锐角、钝角或直角).
总是__________(填锐角、钝角或直角).
③若过![]() 点作
点作![]() 于
于![]() ,你能猜想
,你能猜想![]() 与
与![]() 之间的数量关系吗?说明理由.(在(1)中的图上作
之间的数量关系吗?说明理由.(在(1)中的图上作![]() 于
于![]() )
)
【答案】(1)见解析;(2)①![]() ;②锐角;③
;②锐角;③![]() ,理由见解析
,理由见解析
【解析】
(1)根据要求画出图形即可;
(2)①当∠ACB=40°时,根据角平分线定义及三角形外角的性质求出∠AIF,然后可得∠BFC,同理求出其他两种情况;
②根据∠BFC=∠AIF=90°-![]() ∠ACB,得出∠BFC<90°,即可判断;
∠ACB,得出∠BFC<90°,即可判断;
③利用直角三角形两锐角互余可得![]() ,结合
,结合![]() 可得答案.
可得答案.
解:(1)如图所示;
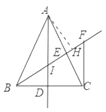
(2)①∵AD,BE是△ABC的角平分线,
∴∠BAI=![]() ∠BAC,∠ABI=
∠BAC,∠ABI=![]() ∠ABC,
∠ABC,
∴∠AIF=∠ABI+∠ABI=![]() (∠BAC+∠ABC)=
(∠BAC+∠ABC)=![]() (180°-∠ACB)=90°-
(180°-∠ACB)=90°-![]() ∠ACB,
∠ACB,
∴当∠ACB=40°时,∠AIF=70°,
∵CF∥AD,
∴∠BFC=∠AIF=70°,
同法可得:当∠ACB=90°时,∠BFC=45°,
当∠ACB=110°时,∠BFC=35°,
故答案为70°,45°,35°;
②∵∠BFC=∠AIF=90°-![]() ∠ACB,
∠ACB,
∴∠BFC<90°,
∴∠BFC总是锐角;
③如图,过![]() 点作
点作![]() 于
于![]() ;
;
结论:![]() ,
,
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数有( )
①已知直角三角形的面积为2,两直角边的比为1:2,则斜边长为![]() ;
;
②直角三角形的最大边长为![]() ,最短边长为1,则另一边长为
,最短边长为1,则另一边长为![]() ;
;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC为直角三角形;
④等腰三角形面积为12,底边上的高为4,则腰长为5.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC绕点B逆时针旋转到△A′BC′,使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为cm2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
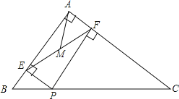
【题目】Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等腰三角形,AB=AC,点D为直线BC上一动点(点D不与点B、点C重合).以AD为边作△ADE,且AD=AE,连接CE,∠BAC=∠DAE.
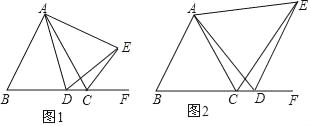
(1)如图1,当点D在边BC上时,试说明:①△ABD≌△ACE;②BC=DC+CE;
(2)如图2,当点D在边BC的延长线上时,其他条件不变,探究线段BC、DC、CE之间存在的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐乐发现等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形底角的度数为( )
A.50°B.65°C.65°或25°D.50°或40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图甲,AB∥CD,试问∠2与∠1+∠3的关系是什么,为什么?
(2)如图乙,AB∥CD,试问∠2+∠4与∠1+∠3+∠5一样大吗?为什么?
(3)如图丙,AB∥CD,试问∠2+∠4+∠6与∠1+∠3+∠5+∠7哪个大?为什么?
你能将它们推广到一般情况吗?请写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好.
(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2 , 并指出她与嘉嘉抽到勾股数的可能性一样吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com