
【题目】随着“一带一路”的进一步推进,我国瓷器(“china”)更为“一带一路”沿线人民所推崇,一外国商户看准这一商机,向我国一瓷器经销商咨询工艺品茶具,得到如下信息:
(1)每个茶壶的批发价比茶杯多110元;
(2)一套茶具包括一个茶壶与四个茶杯;
(3)600元批发茶壶的数量与160元批发茶杯的数量相同.
根据以上信息:求茶壶与茶杯的批发价
(1)求茶壶与茶杯的批发价;
(2)若该商户购进茶杯的数量是茶壶数量的5倍还多20个,并且茶壶数量不超过30个,该商户打算将茶具按每套500元成套销售,剩余的茶杯每个70元零售,应如何进货才能使这批茶具获利最多?并求出最大利润.
【答案】(1) 茶杯的批发价为40元/个,则茶壶的批发价为150元/个;(2) 当购进30个茶壶、170个茶杯时,有最大利润,最大利润为7200元
【解析】
(1)设茶杯的批发价为x元/个,则茶壶的批发价为(x+110)元/个,根据数量=总价÷单价结合600元批发茶壶的数量与160元批发茶杯的数量相同,即可得出关于x的分式方程,解之并检验后即可得出结论;
(2)设商户购进茶壶m个,则购进茶杯(5m+20)个,设利润为w,根据总利润=单件利润×销售数量结合销售方式,即可得出w关于m的函数关系式,利用一次函数的性质即可解决最值问题.
(1)设茶杯的批发价为x元/个,则茶壶的批发价为(x+110)元/个,
根据题意得:![]() ,
,
解得:x=40,
经检验,x=40是原分式方程的解,
∴x+110=150.
答:茶杯的批发价为40元/个,则茶壶的批发价为150元/个.
(2)设商户购进茶壶m个,则购进茶杯(5m+20)个,
若利润为w元,则w=m(500﹣150﹣4×40)+(5m+20﹣4m)×(70﹣40)=220m+600,
∵w随着m的增大而增大,
∴当m取最大值时,利润w最大,
∵m≤30,
∴当m=30时,w=7200.
∴当购进30个茶壶、170个茶杯时,有最大利润,最大利润为7200元.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
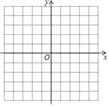
【题目】在平面直角坐标系中(如图每格一个单位),描出下列各点A(﹣2,﹣1),B(2,﹣1),C(2,2),D(3,2),E(0,3),F(﹣3,2),G(﹣2,2),A(﹣2,﹣1)并依次将各点连接起来,观察所描出的图形,它像什么?根据图形回答下列问题:
(1)图形中哪些点在坐标轴上,它们的坐标有什么特点?
(2)线段FD和x轴有什么位置关系?点F和点D的坐标有什么特点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知2x﹣y=8,求代数式[x2+y2﹣(x﹣y)2+2y(x﹣y)]÷4y的值.
(2)阅读下列材料:常用分解因式的方法有提取公因式法、公式法,但有部分多项式只单纯用上述方法就无法分解,如x2﹣2xy+y2﹣16,我们细心观察这个式子就会发现,前三项符合完全平方公式,进行变形后可以与第四项结合再运用平方差公式进行分解.过程如下:x2﹣2xy+y2﹣16=(x﹣y)2﹣16=(x﹣y+4)(x﹣y﹣4)这种分解因式的方法叫分组分解法.利用这种分组的思想方法解决下列问题:
已知a,b,c分别是△ABC三边的长,且2a2+b2+c2﹣2a(b+c)=0请判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 . 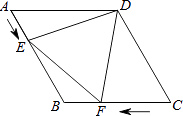
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以图1(以O为圆心,半径1 的半圆)作为“基本图形”,分别经历如下变换能得到图2的序号是 (多填或错填得0分,少填酌情给分)
①只要向右平移1个 单位;
② 先以直线AB为对称轴进行对称变换,再向右平移1个单位;
③先绕着O旋转180°,再向右平移1个单位;
④只要绕着某点旋转180°.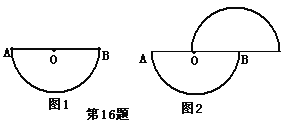
查看答案和解析>>
科目:初中数学 来源: 题型:
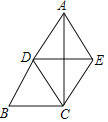
【题目】已知:如图,在△ABC中,∠ACB=90°,点D是斜边AB的中点,DE∥BC,且CE=CD.
(1)求证:∠B=∠DEC;
(2)求证:四边形ADCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
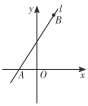
【题目】如图,已知直线l经过点A(-1,0)和点B(1,4).
(1)求直线l的解析式;
(2)若点P是x轴上的点,且△APB的面积为8,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
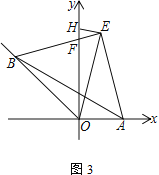
【题目】在平面直角坐标系中,![]() ,点
,点![]() 在第二象限的角平分线上,
在第二象限的角平分线上,![]() 、
、![]() 的垂直平分线交于点
的垂直平分线交于点![]() .
.
(1)求证:![]() ;
;
(2)设![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)作![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,求
,求![]() 点的坐标.
点的坐标.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com