
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 . 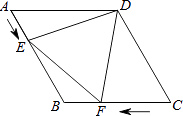
【答案】![]()
【解析】 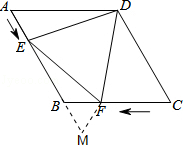
解:延长AB至M,使BM=AE,连接FM,
∵四边形ABCD是菱形,∠ADC=120°
∴AB=AD,∠A=60°,
∵BM=AE,
∴AD=ME,
∵△DEF为等边三角形,
∴∠DAE=∠DFE=60°,DE=EF=FD,
∴∠MEF+∠DEA═120°,∠ADE+∠DEA=180°﹣∠A=120°,
∴∠MEF=∠ADE,
∴在△DAE和△EMF中,
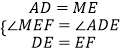
∴△DAE≌EMF(SAS),
∴AE=MF,∠M=∠A=60°,
又∵BM=AE,
∴△BMF是等边三角形,
∴BF=AE,
∵AE=t,CF=2t,
∴BC=CF+BF=2t+t=3t,
∵BC=4,
∴3t=4,
∴t= ![]()
故答案为: ![]() .
.
延长AB至M,使BM=AE,连接FM,证出△DAE≌EMF,得到△BMF是等边三角形,再利用菱形的边长为4求出时间t的值.


科目:初中数学 来源: 题型:
【题目】在一节数学课上,刘老师请同学们心里想一个非零的有理数,然后把这个数按照下面的程序进行计算后,刘老师立刻说出计算结果.

(1)若小明同学心里想的数是8,请列出算式并计算最后的结果;
(2)小明又试了几个数进行计算,发现结果都相等,于是小明把心里想的这个数记作a(a≠0),并按照程序通过计算进行验证,请你写出这个验证过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个粒子在第一象限内及x轴、y轴上运动,在第一分钟,它从原点运动到点(1,0),第二分钟,它从点(1,0)运动到点(1,1),而后它接着按图中箭头所示在与x轴,y轴平行的方向上来回运动,且每分钟移动1个单位长度,那么在第2019分钟时,这个粒子所在位置的坐标是( )
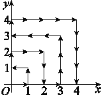
A. (44,5) B. (5,44) C. (44,6) D. (6,44)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为( ) 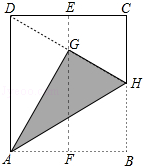
A.2cm
B.2 ![]() cm
cm
C.4cm
D.4 ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:![]()
![]()
![]()
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
(3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“一带一路”的进一步推进,我国瓷器(“china”)更为“一带一路”沿线人民所推崇,一外国商户看准这一商机,向我国一瓷器经销商咨询工艺品茶具,得到如下信息:
(1)每个茶壶的批发价比茶杯多110元;
(2)一套茶具包括一个茶壶与四个茶杯;
(3)600元批发茶壶的数量与160元批发茶杯的数量相同.
根据以上信息:求茶壶与茶杯的批发价
(1)求茶壶与茶杯的批发价;
(2)若该商户购进茶杯的数量是茶壶数量的5倍还多20个,并且茶壶数量不超过30个,该商户打算将茶具按每套500元成套销售,剩余的茶杯每个70元零售,应如何进货才能使这批茶具获利最多?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.
(1)求证:OF∥BE;
(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(3)延长DC、FP交于点G,连接OE并延长交直线DC于H(图2),问是否存在点P,使△EFO∽△EHG(E、F、O与E、H、G为对应点)?如果存在,试求(2)中x和y的值;如果不存在,请说明理由.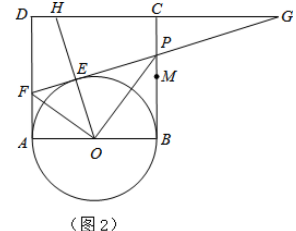
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义新运算:对于任意实数a,b,都有a⊕b=a(a﹣b)+1,等式右边是通常的加法,减法及乘法运算.比如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5
(1)求3⊕(﹣2)的值;
(2)若3⊕x的值小于16,求x的取值范围,并在数轴上表示出来.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com