
【题目】如图1,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.
(1)求证:OF∥BE;
(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(3)延长DC、FP交于点G,连接OE并延长交直线DC于H(图2),问是否存在点P,使△EFO∽△EHG(E、F、O与E、H、G为对应点)?如果存在,试求(2)中x和y的值;如果不存在,请说明理由.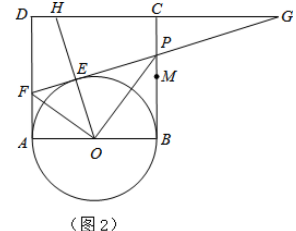
【答案】
(1)
证明:连接OE
FE、FA是⊙O的两条切线
∴∠FAO=∠FEO=90°
在Rt△OAF和Rt△OEF中,
![]()
∴Rt△FAO≌Rt△FEO(HL),
∴∠AOF=∠EOF= ![]() ∠AOE,
∠AOE,
∴∠AOF=∠ABE,
∴OF∥BE

(2)
解:过F作FQ⊥BC于Q
∴PQ=BP﹣BQ=x﹣y
PF=EF+EP=FA+BP=x+y
∵在Rt△PFQ中
∴FQ2+QP2=PF2
∴22+(x﹣y)2=(x+y)2
化简得: ![]() ,(1<x<2)
,(1<x<2)
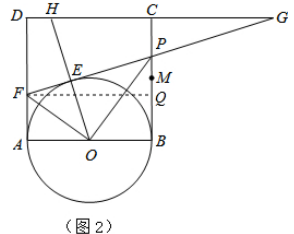
(3)
解:存在这样的P点,
理由:∵∠EOF=∠AOF,
∴∠EHG=∠EOA=2∠EOF,
当∠EFO=∠EHG=2∠EOF时,
即∠EOF=30°时,Rt△EFO∽Rt△EHG,
此时Rt△AFO中,
y=AF=OAtan30°= ![]() ,
,
∴ ![]()
∴当 ![]() 时,△EFO∽△EHG
时,△EFO∽△EHG
【解析】(1)首先证明Rt△FAO≌Rt△FEO进而得出∠AOF=∠ABE,即可得出答案;(2)过F作FQ⊥BC于Q,利用勾股定理求出y与x之间的函数关系,根据M是BC中点以及BC=2,即可得出BP的取值范围;(3)首先得出当∠EFO=∠EHG=2∠EOF时,即∠EOF=30°时,Rt△EFO∽Rt△EHG,求出y=AF=OAtan30°= ![]() ,即可得出答案.
,即可得出答案.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
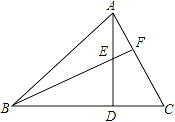
【题目】如图,在△ABC中,AD⊥BC于D,BF与AD相交于E.若AD=BD,BE=AC,BC=8cm,DC=3cm,则AE=_____,∠BFC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 . 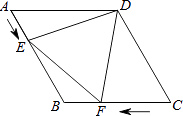
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球(每个气排球的价格都相同,每个篮球的价格都相同).经洽谈,购买1个气排球和2个篮球共需210元;购买2个气排球和3个篮球共需340元.
(1)每个气排球和每个篮球的价格各是多少元?
(2)该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个,总费用不超过3200元,且购买气排球的个数少于30个,应选择哪种购买方案可使总费用最低?最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
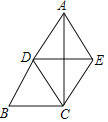
【题目】已知:如图,在△ABC中,∠ACB=90°,点D是斜边AB的中点,DE∥BC,且CE=CD.
(1)求证:∠B=∠DEC;
(2)求证:四边形ADCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组: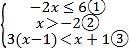 .
.
请结合题意,完成本题的解答.
(1)解不等式①,得 ,依据是: .
(2)解不等式③,得 .
(3)把不等式①,②和③的解集在数轴上表示出来.
![]()
(4)从图中可以找出三个不等式解集的公共部分,得不等式组的解集 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条不完整的数轴上,从左向右有两个点A、B,其中A点表示的数为m,B表示数的为4,点C也为数轴上一点,且AB=2AC,
(1)若m为整数,求m的最大值;
(2)若C表示的数为﹣2,求m的值;
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com