
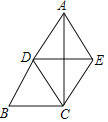
【题目】已知:如图,在△ABC中,∠ACB=90°,点D是斜边AB的中点,DE∥BC,且CE=CD.
(1)求证:∠B=∠DEC;
(2)求证:四边形ADCE是菱形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据直角三角形斜边上的中线等于斜边的一半,得到DB=DC,从而∠B=∠DCB,由DE∥BC,得到∠DCB=∠CDE,由CE=CD,得到∠CDE=∠DEC,利用等量代换,得到∠B=∠DEC;
(2)先利用一组对边平行且相等的四边形是平行四边形,证明四边形ADCE是平行四边形,再由CD=CE,证明平行四边形ADCE是菱形.
(1)证明:在△ABC中,∵∠ACB=90°,点D是斜边AB的中点,
∴CD=DB,
∴∠B=∠DCB,
∵DE∥BC,
∴∠DCB=∠CDE,
∵CD=CE,
∴∠CDE=∠CED,
∴∠B=∠CED.
(2)证明:∵DE∥BC,
∴∠ADE=∠B,
∵∠B=∠DEC,
∴∠ADE=∠DEC,
∴AD∥EC,
∵EC=CD=AD,
∴四边形ADCE是平行四边形,
∵CD=CE,
∴四边形ADCE是菱形.
故答案为:(1)证明见解析;(2)证明见解析.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且AE=![]() (AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.
(AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.
解:猜想: .
证明:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为( ) 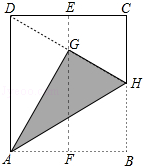
A.2cm
B.2 ![]() cm
cm
C.4cm
D.4 ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“一带一路”的进一步推进,我国瓷器(“china”)更为“一带一路”沿线人民所推崇,一外国商户看准这一商机,向我国一瓷器经销商咨询工艺品茶具,得到如下信息:
(1)每个茶壶的批发价比茶杯多110元;
(2)一套茶具包括一个茶壶与四个茶杯;
(3)600元批发茶壶的数量与160元批发茶杯的数量相同.
根据以上信息:求茶壶与茶杯的批发价
(1)求茶壶与茶杯的批发价;
(2)若该商户购进茶杯的数量是茶壶数量的5倍还多20个,并且茶壶数量不超过30个,该商户打算将茶具按每套500元成套销售,剩余的茶杯每个70元零售,应如何进货才能使这批茶具获利最多?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.
(1)求证:OF∥BE;
(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(3)延长DC、FP交于点G,连接OE并延长交直线DC于H(图2),问是否存在点P,使△EFO∽△EHG(E、F、O与E、H、G为对应点)?如果存在,试求(2)中x和y的值;如果不存在,请说明理由.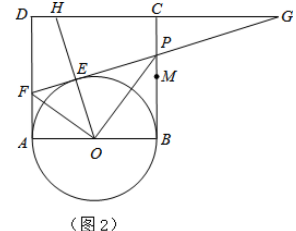
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若直线l1经过点(0,4),l2经过(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为
A. (-2,0) B. (2,0) C. (-6,0) D. (6,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三个天平的托盘中形状相同的物体质量相等.图①、图②所示的两个天平处于平衡状态,要使第三个天平也保持平衡,可在它的右盘中放置( )

A. 3个球 B. 4个球
C. 5个球 D. 6个球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,下列条件中,不能说明AB⊥CD的是( )

A. ∠AOD=90°
B. ∠AOC=∠BOC
C. ∠BOC+∠BOD=180°
D. ∠AOC+∠BOD=180°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com