
【题目】如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,BD分别与AE、AF相交于G、H.

(1)在图中找出与△ABE相似的三角形,并说明理由;
(2)若AG=AH,求证:四边形ABCD是菱形.
【答案】(1)△ABE∽△ADF.(2)证明见解析.
【解析】
试题(1)根据两角对应相等可证出△ABE∽△ADF;
(2)由(1)的结论,先证出△ABG≌△ADH,得到AB=AD,那么平行四边形ABCD是菱形.
试题解析:(1)△ABE∽△ADF.理由如下:
∵AE⊥BC于E,AF⊥CD于F,∴∠AEB=∠AFD=90°.
∵四边形ABCD是平行四边形,∴∠ABE=∠ADF.
∴△ABE∽△ADF.
(2)∵AG=AH,∴∠AGH=∠AHG.∴∠AGB=∠AHD.
∵△ABE∽△ADF,∴∠BAG=∠DAH.
∴∠BAG≌∠DAH.∴AB=AD .
∵四边形ABCD是平行四边形,AB=AD,∴平行四边形ABCD是菱形.


科目:初中数学 来源: 题型:
【题目】如图,在五边形 ABCDE 中,∠A+∠B+∠E=α,DP,CP 分别平分∠EDC,∠BCD,则∠P 的度数是( )

A. 90°+![]() α B.
α B. ![]() α﹣90° C.
α﹣90° C. ![]() α D. 540° -
α D. 540° -![]() α
α
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的直径AB=4,点C在⊙O上,连接AC,沿AC折叠劣弧![]() ,记折叠后的劣弧为
,记折叠后的劣弧为![]() .
.
(1)如图1,当![]() 经过圆心O时,求
经过圆心O时,求![]() 的长.
的长.
(2)如图2,当![]() 与AB相切于A时.
与AB相切于A时.
①画出![]() 所在的圆的圆心P.
所在的圆的圆心P.
②求出阴影部分弓形![]() 的面积.
的面积.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,一直线y=2x+b经过点A(-1,0)与y轴正半轴交于B点,在x轴正半轴上有一点D,且OB=OD,过D点作DC⊥x轴交直线y=2x+b于C点,反比例函数y=![]() (x>O)经过点C.
(x>O)经过点C.

(1)求b,k的值;
(2)求△BDC的面积;
(3)在反比例函数y=![]() (x>0)的图象上找一点P(异于点C),使△BDP与△BDC的面积相等,求出P点坐标.
(x>0)的图象上找一点P(异于点C),使△BDP与△BDC的面积相等,求出P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格(元/个)的函数关系如图所示.
(1)当30≤x≤60时,求y与x的函数关系式;
(2)求出该厂生产销售这种产品的纯利润w(万元)与销售价格x(元/个)的函数关系式;
(3)销售价格应定为多少元时,获得利润最大,最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,P是BC边上一动点(点P不与B、C重合),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA、NA,则以下结论:①△CMP∽△BPA;②四边形AMCB的面积最大值为2.5;③△ADN≌△AEN;④线段AM的最小值为2.5;⑤当P为BC中点时,AE为线段NP的中垂线.正确的有_____(只填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,甲、乙两个容器内都装了一定数量的水,现将甲容器中的水匀速注入乙容器中.图2中的线段AB,CD分别表示容器中的水的深度h(厘米)与注入时间t(分钟)之间的函数图象.下列结论错误的是( )
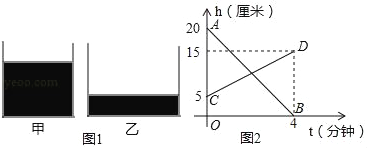
A. 注水前乙容器内水的高度是5厘米
B. 甲容器内的水4分钟全部注入乙容器
C. 注水2分钟时,甲、乙两个容器中的水的深度相等
D. 注水1分钟时,甲容器的水比乙容器的水深5厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是∠AOB内一点,点E,F分别在OA,OB上,且OE<OF,DE=DF,∠OED+∠OFD=180°,

(1)请作出点D到OA,OB的距离,标明垂足;
(2)求证:OD平分∠AOB;
(3)若∠AOB=60°,OD=6,OE=4,求△ODE的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,等腰Rt△OAB中,∠AOB=90°,等腰Rt△EOF中,∠EOF=90°,连结AE、BF.

求证:(1)AE=BF;(2)AE⊥BF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com