解:(1)k的值为6,k′的值为

;点B的坐标为(-3,-2);
(2)由题意可知,m(m+1)=(m+3)(m-1)=k,解得m=3;
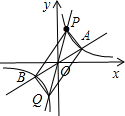
(3)①证明:由m=3得A(3,2),P(1,6),
由此可得:B(-3,-2),Q(-1,-6),
∴
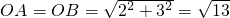
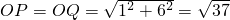
,
∴四边形APBQ是平行四边形;
②存在两种情况,如图:
(a)当M点在x轴的正半轴上,N点在y轴的正半轴上时,
设M
1点坐标为(x
1,0),N
1点坐标为(0,y
1),
∵四边形AN
1M
1B为平行四边形,
∴线段N
1M
1可看作由线段PA向左平移1个单位,再向下平移2个单位得到的,
(也可看作向下平移2个单位,再向左平移1个单位得到的).
又A点坐标为(3,2),P点坐标为(1,6),
∴N
1点坐标为(0,6-2),即N
1(0,4),
M
1点坐标为(3-1,0),即M
1(2,0);
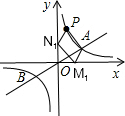
(b)当M点在x轴的负半轴上,N点在y轴的负半轴上时,
设M
2点坐标为(x
2,0),N
2点坐标为(0,y
2),
∵PA∥N
1M
1,PA∥M
2N
2,PA=N
1M
1,PA=M
2N
2,
∴N
1M
1∥M
2N
2,N
1M
1=M
2N
2,
∴0M
2=OM
1,ON
1=ON
2,
∴M
2点坐标为(-2,0),N
2点坐标为(0,-4).
注意:没写过程的:只写出一种情况坐标得,写两种得过程不必这样细.
分析:(1)把点A的坐标为(3,2),分别代入解析式

(k>0)与直线y=k′x,就可以求出k与k′的值.解两个函数的解析式组成的方程组就得到B点的坐标;
(2)若点A(m,m-1),P(m-2,m+3)都在双曲线的图象上.把这两点代入函数解析式就可以得到关于m的方程,可以求出m的值;
(3)①根据反比例函数是中心对称图形,得到OA=OB,OP=OQ,则四边形APBQ的两条对角线互相平分,因而四边形APBQ是平行四边形;
②存在两种情况,当M点在x轴的正半轴上,N点在y轴的正半轴上时,根据四边形AN
1M
1B为平行四边形,根据直线的平移就可以得到M
1点的坐标.当M点在x轴的负半轴上,N点在y轴的负半轴上时,同理可以得到M
2点和N
2点的坐标.
点评:本题主要考查了待定系数法求函数的解析式,并且反比例函数的图象是中心对称图形.

 (k>0)与直线y=k′x交于A,B两点,点P在第一象限.
(k>0)与直线y=k′x交于A,B两点,点P在第一象限.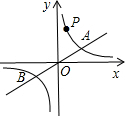
 ;点B的坐标为(-3,-2);
;点B的坐标为(-3,-2);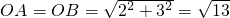
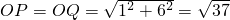 ,
,

 (k>0)与直线y=k′x,就可以求出k与k′的值.解两个函数的解析式组成的方程组就得到B点的坐标;
(k>0)与直线y=k′x,就可以求出k与k′的值.解两个函数的解析式组成的方程组就得到B点的坐标;

 如图,已知双曲线y1=
如图,已知双曲线y1= (2012•济南)如图,已知双曲线y=
(2012•济南)如图,已知双曲线y= (2013•徐州模拟)如图,已知双曲线y=
(2013•徐州模拟)如图,已知双曲线y= 如图,已知双曲线y=
如图,已知双曲线y=