
【题目】如图,点P、M、N分别在等边△ABC的各边上,且MP⊥AB于点P,MN⊥BC于点M,PV⊥AC于点N,若AB=12cm,求CM的长为______cm.
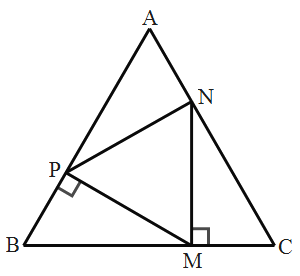
【答案】4
【解析】
根据等边三角形的性质得出∠A=∠B=∠C,进而得出∠MPB=∠NMC=∠PNA=90°,根据平角的义即可得出∠NPM=∠PMN=∠MNP,即可证△PMN是等边三角形:根据全等三角形的性质得到PA=BM=CN,PB=MC=AN,从而求得MC+NC=AC=12cm,再根据直角三角形30°角所对的直角边等于斜边的一半得出2MC=NC,即司得MC的长.
∵△ABC是等边三角形,∴∠A=∠B=∠C.
∵MP⊥AB,MN⊥BC,PN⊥AC,∴∠MPB=∠NMC=∠PNA=90°,
∴∠PMB=∠MNC=∠APN,∠NPM=∠PMN=∠MNP,
∴△PMN是等边三角形∴PN=PM=MN,∴△PBM≌△MCN≌△NAP(AAS),
∴PA=BM=CN,PB=MC=AN,MC+NC=AC=12cm,
∵∠C=60°,∴∠MNC=30°,
∴NC=2CM,∴MC+NC=3CM=12cm,∴CM=4cm.
故答案为:4cm


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】某学校计划选购![]() 、
、![]() 两种图书.已知
两种图书.已知![]() 种图书每本价格是
种图书每本价格是![]() 种图书每本价格的2.5倍,用1200元单独购买
种图书每本价格的2.5倍,用1200元单独购买![]() 种图书比用1500元单独购买
种图书比用1500元单独购买![]() 种图书要少25本.
种图书要少25本.
(1)![]() 、
、![]() 两种图书每本价格分别为多少元?
两种图书每本价格分别为多少元?
(2)如果该学校计划购买![]() 种图书的本数比购买
种图书的本数比购买![]() 种图书本数的2倍多8本,且用于购买
种图书本数的2倍多8本,且用于购买![]() 、
、![]() 两种图书的总经费不超过1164元,那么该学校最多可以购买多少本
两种图书的总经费不超过1164元,那么该学校最多可以购买多少本![]() 种图书?
种图书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从一副52张(没有大小王)的扑克牌中,每次抽出1张,然后放回洗匀再抽,在试验中得到下表中部分数据:
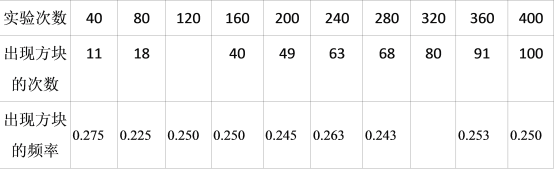
(1)将数据表补充完整;
(2)从上表中可以估计出现方块的概率是________(精确到0.01);
(3)从这副扑克牌中取出两组牌,分别是方块1,2,3和红桃1,2,3,将它们背面朝上分别重新洗牌后,从两组牌中各摸出一张,若摸出的两张牌的牌面数字之和等于3,则甲方赢;若摸出的两张牌的牌面数字之和等于4,则乙方赢.你认为这个游戏对双方是公平的吗?若不是,有利于谁?请你用概率知识(列表法或画树状图法)加以分析说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识改变世界,科技改变生活.导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地13千米,导航显示车辆应沿北偏东60°方向行驶至B地,再沿北偏西37°方向行驶一段距离才能到达C地,求B、C两地的距离.(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
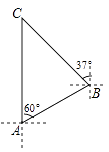
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用两个全等的等边△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺60°角的项点与点A重合,两边分别与AB、AC重合,将三角尺绕点A按逆时针方向旋转.当三角尺的两边分别与菱形的两边BC、CD相交于点E、F时(如图),通过观察或测量BE、CF的长度,你能得出什么结论?并证明你的结论.
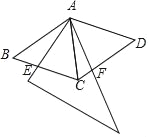
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.



(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论中,错误的有( )
①在Rt△ABC中,已知两边长分别为3和4,则第三边的长为5;
②△ABC的三边长分别为AB,BC,AC,若![]() +
+![]() =
=![]() ,则∠A=90°;
,则∠A=90°;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④若三角形的三边长之比为3:4:5,则该三角形是直角三角形.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com