练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】甲、乙两车分别从A、B两地同时出发匀速相向而行，大楼C位于AB之间，甲与乙相遇在AC中点处，然后两车立即掉头，以原速原路返回，直到各自回到出发点．设甲、乙两车距大楼C的距离之和为y（千米），甲车离开A地的时间为t（小时），y与t的函数图象所示，则第21小时时，甲乙两车之间的距离为________千米．

    【答案】1350

    【解析】解：设AC中点为E．观察函数图象可知：乙车从B到C需用4小时，从C到E需用（20-4）÷2=8小时，甲从A到E需要12小时．

    ∵点E为AC的中点，乙的速度不变，∴AE=CE=2BC（如图所示）．

    ∵2CE=1440，∴AE=720，BE=1080，∴甲的速度为720÷12=60（千米/小时），乙的速度为1080÷12=90（千米/小时）．

    第21小时时，甲乙两车之间的距离为（60+90）×（21﹣12）=1350（千米）．

    故答案为：1350．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示的图像反映的过程是：甲乙两人同时从地出发,以各自的速度匀速向地行驶，甲先到地停留半小时后，按原路以另一速度匀速返回,直至与乙相遇.乙的速度为， 表示甲乙两人相距的距离， 表示乙行驶的时间.现有以下个结论：①、两地相距；②点的坐标为；③甲去时的速度为；④甲返回的速度是.以上个结论中正确的是_______________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解分式方程、分式的化简求值

    （1） ；

    （2） ；

    （3），其中 ；

    （4），其中x是不等式组的解集中符合题意的整数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

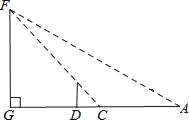
    【题目】小明是个爱动脑筋的学生，在学习了解直角三角形以后，一天他去测量学校的旗杆GF的高度，此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米．

    （1）若旗杆的高度FG是a米，用含a的代数式表示DG．

    （2）小明从点C后退6米在A的测得旗杆顶点F的仰角为30°，求旗杆FG的高度．（点A、C、D、G在一条直线上， ， ，结果精确到0.1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商家用1200元购进了一批T恤，上市后很快售完，商家又用2800元购进了第二批这种T恤，所购数量是第一批购进量的2倍，但单价贵了5元．

    （1）该商家购进的第一批T恤是多少件？

    （2）若两批T恤按相同的标价销售，最后剩下20件按八折优惠卖出，如果希望两批T恤全部售完的利润率不低于16%（不考虑其它因素），那么每件T恤的标价至少是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了加强对校内外的安全监控，创建平安校园，某学校计划增加台监控摄像设备，现有甲、乙两种型号的设备，其中每台价格、有效监控半径如表所示，经调查，购买台甲型设备比购买台乙型设备少元，购买台甲型设备比购买台乙型设备多元.

    甲型

    乙型

    价格（元/台）

    有效半径（米/台）

    （）求，的值；

    （）若购买该批设备的资金不超过元，且两种型号的设备均要至少买一台，学校有哪几种购买方案？

    （）在（）的条件下，若要求监控半径覆盖范围不低于米，为了节约资金，请你设计一种最省钱的购买方案.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1） [探索发现]正方形中,是对角线上的一个动点(与点不重合),过点作交线段于点．求证:

    小玲想到的思路是:过点作于点于点,通过证明得到．请按小玲的思路写出证明过程

    （2）[应用拓展]如图2,在的条件下，设正方形的边长为,过点作交于点．求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知等腰Rt△ABC，∠ACB=90°，CA=CB，以BC为边向外作等边△CBA，连接AD，过点C作∠ACB的角平分线与AD交于点E，连接BE．

    （1）若AE=2，求CE的长度；

    （2）以AB为边向下作△AFB，∠AFB=60°，连接FE，求证：FA+FB= FE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线与反比例函数的图象交于点，与轴交于点，与轴交于点，垂直轴于点，且．

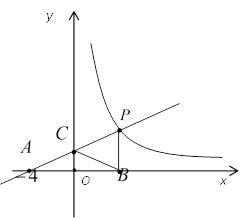
    （1）仔细观察图形，直接写出；

    （2）求和的值；

    （3）在反比例函数图象上是否存在点，使四边形为平行四边形，如果存在，求出点的坐标，如果不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案