【题目】为了加强对校内外的安全监控，创建平安校园，某学校计划增加台监控摄像设备，现有甲、乙两种型号的设备，其中每台价格、有效监控半径如表所示，经调查，购买台甲型设备比购买台乙型设备少元，购买台甲型设备比购买台乙型设备多元.

甲型

乙型

价格（元/台）

有效半径（米/台）

（）求，的值；

（）若购买该批设备的资金不超过元，且两种型号的设备均要至少买一台，学校有哪几种购买方案？

（）在（）的条件下，若要求监控半径覆盖范围不低于米，为了节约资金，请你设计一种最省钱的购买方案.

参考答案：

【答案】（1）；（2）学校有三种购买方案：方案一甲台乙台；方案二甲台乙台；方案三甲台乙台；（3）最省钱的购买方法为购买甲台，乙台．

【解析】

（1）根据“购买1台甲型设备比购买1台乙型设备少150元，购买3台甲型设备比购买2台乙型设备多150元”，即可得出关于a，b的二元一次方程组，解之即可得出结论；

（2）设购买甲型设备x台，则购买乙型设备（15-x）台，根据总价=单价×数量结合购买该批设备的资金不超过7200元且两种型号的设备均要至少买一台，即可得出关于x的一元一次不等式组，解之即可得出x的取值范围，再结合x为整数即可得出各购买方案；

（3）由（2）的结论结合监控半径覆盖范围不低于1600米，可求出x的值，再利用总价=单价×数量可求出当x=12和x=13时购买费用，比较后即可得出结论．

解：（1）由题意得,

解得;

（2）设购买甲型设备台，则购买乙型设备台,

由题意得

，

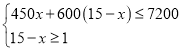解得

∵取整数，∴，，共三种方案，

答：学校有三种购买方案：方案一甲台乙台；方案二甲台乙台；

方案三甲台乙台．

（3）由题意

解得∴

的取值为或

当时，所需资金为：（元），

当时，所需资金为：（元），

∵，

∴方案二省钱

答：最省钱的购买方法为购买甲台，乙台．

关闭