
【题目】如图,在菱形![]() 中
中![]() ,E为对角线
,E为对角线![]() 上一点,F是
上一点,F是![]() 延长线上一点,连接
延长线上一点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)若点G为![]() 的中点,连接
的中点,连接![]() ,求证:
,求证:![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据菱形的性质,得到AD=CD,∠ABC=∠ADC=∠ACD=∠CAD=60°,然后根据等式的性质求得∠ADE=∠CDF,从而利用ASA定理判定三角形全等,问题得解;
(2)过点B作BH∥AC,交AG的延长线于点H,根据菱形的性质结合(1)中的结论判定△ABE≌△ADE≌△CDF,利用ASA定理判定△BHG≌△EAG,利用SAS定理判定△ABH≌△ACF,从而得到AH=AF,使问题得解.
解:在菱形ABCD中,∵![]()
∴AD=CD,∠ABC=∠ADC=∠ACD=∠CAD=∠ACB=60°
∴∠DCF=60°
又∵![]()
∴∠ADE+∠EDC=∠CDF+∠EDC=60°
∴∠ADE=∠CDF,
在△ADE和△CDF中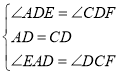
∴△ADE≌△CDF
∴![]() ;
;
(2)过点B作BH∥AC,交AG的延长线于点H
在菱形ABCD中,∠ABE=∠ADE,AB=AD,AE=AE
又由(1)可知△ADE≌△CDF
∴△ABE≌△ADE≌△CDF
∴AE=CF
∵BH∥AC,点G是BE的中点
∴∠H=∠GAE,BG=EG,∠HBG=∠ACB=60°
∴∠ABH=∠ACF=120°
又∵∠AGE=∠HGB
∴△BHG≌△EAG
∴BH=AE=CF,AG=GH
又∵AB=AC
∴△ABH≌△ACF
∴AH=AF=AG+GH=2AG
即![]() .
.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,以
,以![]() 为边在
为边在![]() 外作等边三角形
外作等边三角形![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,与
,与![]() 相交于点
相交于点![]() ,连接
,连接![]() .
.

(1)说明:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 是直线
是直线![]() 上的一点.则当
上的一点.则当![]() 在何处时,
在何处时,![]() 最小,并求此时
最小,并求此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )

A. AE=AC B. ∠B=∠D C. BC=DE D. ∠C=∠E
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=x2+2x+c的图象与x轴交于点A和点B(1,0),以AB为边在x轴上方作正方形ABCD,动点P从点A出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,同时动点Q从点C出发,以每秒1个单位长度的速度沿CB匀速运动,当点Q到达终点B时,点P停止运动,设运动时间为t秒.连接DP,过点P作DP的垂线与y轴交于点E.
(1)求二次函数的解析式及点A的坐标;
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,并求出这个最大值;
(3)在P,Q运动过程中,求当△DPE与以D,C,Q为顶点的三角形相似时t的值;
(4)是否存在t,使△DCQ沿DQ翻折得到△DC′Q,点C′恰好落在抛物线的对称轴上?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中直线![]() :
:![]() 分别与x轴,y轴交于点A和点B,过点A的直线
分别与x轴,y轴交于点A和点B,过点A的直线![]() 与y轴交于点C,
与y轴交于点C,![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)若D为线段![]() 上一点,E为线段
上一点,E为线段![]() 上一点,当
上一点,当![]() 时,求
时,求![]() 的最小值,并求出此时点E的坐标.
的最小值,并求出此时点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
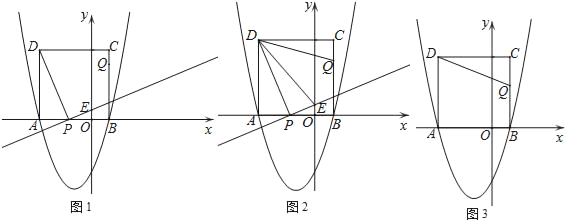
【题目】小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆GF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.
(1)若旗杆的高度FG是a米,用含a的代数式表示DG.
(2)小明从点C后退6米在A的测得旗杆顶点F的仰角为30°,求旗杆FG的高度.(点A、C、D、G在一条直线上, ![]() ,
, ![]() ,结果精确到0.1)
,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强对校内外的安全监控,创建平安校园,某学校计划增加![]() 台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格、有效监控半径如表所示,经调查,购买
台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格、有效监控半径如表所示,经调查,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少
台乙型设备少![]() 元,购买
元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多
台乙型设备多![]() 元.
元.
甲型 | 乙型 | |
价格(元/台) |
|
|
有效半径(米/台) |
|
|
(![]() )求
)求![]() ,
,![]() 的值;
的值;
(![]() )若购买该批设备的资金不超过
)若购买该批设备的资金不超过![]() 元,且两种型号的设备均要至少买一台,学校有哪几种购买方案?
元,且两种型号的设备均要至少买一台,学校有哪几种购买方案?
(![]() )在(
)在(![]() )的条件下,若要求监控半径覆盖范围不低于
)的条件下,若要求监控半径覆盖范围不低于![]() 米,为了节约资金,请你设计一种最省钱的购买方案.
米,为了节约资金,请你设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON.
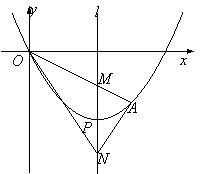
(1)求该二次函数的关系式;
(2)若点A的坐标是(6,-3),求△ANO的面积;
(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com