
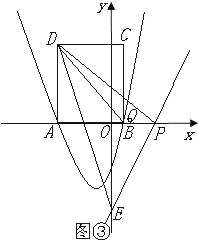
【题目】如图,二次函数y=x2+2x+c的图象与x轴交于点A和点B(1,0),以AB为边在x轴上方作正方形ABCD,动点P从点A出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,同时动点Q从点C出发,以每秒1个单位长度的速度沿CB匀速运动,当点Q到达终点B时,点P停止运动,设运动时间为t秒.连接DP,过点P作DP的垂线与y轴交于点E.
(1)求二次函数的解析式及点A的坐标;
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,并求出这个最大值;
(3)在P,Q运动过程中,求当△DPE与以D,C,Q为顶点的三角形相似时t的值;
(4)是否存在t,使△DCQ沿DQ翻折得到△DC′Q,点C′恰好落在抛物线的对称轴上?若存在,请求出t的值;若不存在,请说明理由.
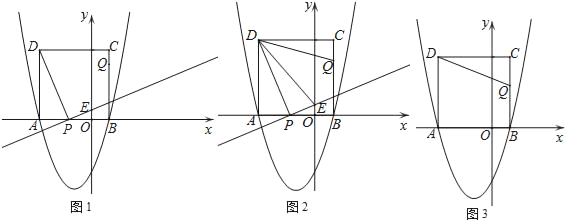
【答案】(1)y=x2+2x﹣3,点A的坐标为(﹣3,0);
(2)点P位于AO的中点时,线段OE的长有最大值![]() ;
;
(3)t=1或3或![]() ,
,
(4)存在t=![]() .
.
【解析】试题分析:(1)先将点B的坐标代入解析式求得c的值确定二次函数解析式,令y=0即可求得A点坐标.
(2)由DP⊥PE证得△DAP∽△POE,用比例式表示出y与t的关系,根据函数图象的性质可求得OE的最大值.
(3)需要分类讨论:根据t的不同取值得出相似三角形,再由相似的性质可得t的取值.
(4)先证明△DCQ≌DC′Q,从而得到∠CDQ=∠C′DQ,DC′=DC=4,再得出∠CDQ=30°,即可求得满足条件的t值.
解:(1)把B(1,0)代入y=x2+2x+c得c=﹣3,
∴y=x2+2x﹣3,
由x2+2x﹣3=0得x1=﹣3,x2=1,
∴点A的坐标为(﹣3,0).
(2)如图(2),由正方形ABCD得AD=AB=4,
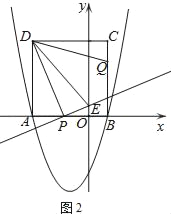
由DP⊥PE证得△DAP∽△POE,
∴![]() ,设OE=y,则
,设OE=y,则![]() ,
,
∴y=![]() =﹣(t﹣
=﹣(t﹣![]() )2+
)2+![]() ,
,
∵a=﹣1<0,
∴当t=![]() 时(属于0<t<
时(属于0<t<![]() )时,y最大=
)时,y最大=![]() ,此时2t=
,此时2t=![]() ,即点P位于AO的中点时,
,即点P位于AO的中点时,
∴线段OE的长有最大值![]() .
.
(3)①如图①,当0<t<![]() 时,△DPE∽△DCQ,
时,△DPE∽△DCQ,
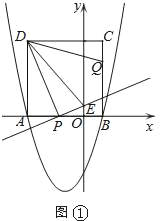
∴![]() .又△ADP∽△OPE,
.又△ADP∽△OPE,
∴![]() ,
,
∴![]() .即
.即![]() ,解得t=1,
,解得t=1,
经检验:t=1是原方程的解.
②如图②,当![]() 时,同理证得△ADP∽△OPE,
时,同理证得△ADP∽△OPE,
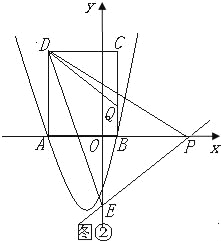
∴![]() ,
,
即![]() ,解得t=3.经检验:t=3是原方程的解.
,解得t=3.经检验:t=3是原方程的解.
③如图③,当![]() 时,△DPE∽△QCD,
时,△DPE∽△QCD,
∴![]() ,
,
同理得![]() ,
,
∴![]() .即
.即![]() ,解得t1=
,解得t1=![]() t2=
t2=![]() (经检验:舍去t2=
(经检验:舍去t2=![]() ),
),
综上所述,t=1或3或![]() ,
,
(4)存在t=![]() .
.
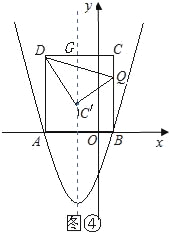
理由如下:如图
由△DCQ沿DQ翻折得△DC′Q,则△DCQ≌△DC′Q,
∴∠CDQ=∠C′DQ,DC′=DC=4,
设抛物线的对称轴交DC于G,则DG=2.在Rt△DC′G中,
∵C′D=2DG,
∴∠C′DG=60°,
∴∠CDQ=![]() ×60°=30°,
×60°=30°,
∴CQ=![]() ,即t=
,即t=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
(1)当t=2时,则AP= ,此时点P的坐标是 。
(2)当t=3时,求过点P的直线l:y=-x+b的解析式?
(3)当直线l:y=-x+b从经过点M到点N时,求此时点P向上移动多少秒?
(4)点Q在x轴时,若S△ONQ=8时,请直按写出点Q的坐标是 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB,根据以下作图过程:
(1)分别以点A、点B为圆心,大于AB长的![]() 为半径作弧,两弧相交于C、D两点;
为半径作弧,两弧相交于C、D两点;
(2)过C、D两点作直线CD.
求证:直线CD是线段AB的垂直平分线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2013年启动省级园林城市创建工作,计划2015年下半年顺利通过验收评审.该市为加快道路绿化及防护绿地等各项建设.在城市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
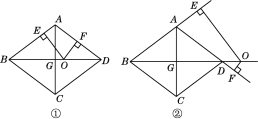
【题目】如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD相交于点G,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)求对角线AC的长及菱形ABCD的面积.
(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由.
(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“阅读素养的培养是构建核心素养的重要基础,重庆十一中学校以‘大阅读’特色课程实施为突破口,着力提升学生的核心素养.”全校师生积极响应和配合,开展各种活动丰富其课余生活.在数学兴趣小组中,同学们从书上认识了很多有趣的数.其中有一个“和平数”引起了同学们的兴趣.描述如下:一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果![]() ,那么称这个四位数为“和平数”.
,那么称这个四位数为“和平数”.
例如:1423,![]() ,
,![]() ,因为
,因为![]() ,所以1423是“和平数”.
,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是________,最大的“和平数”是__________;
(2)求同时满足下列条件的所有“和平数”:
①个位上的数字是千位上的数字的两倍;
②百位上的数字与十位上的数字之和是12的倍数;
(3)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后这两个“和平数”为“相关和平数”.
例如:1423于4132为“相关和平数”
求证:任意的两个“相关和平数”之和是1111的倍数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com