
【题目】如图,![]() 中,
中,![]() ,以
,以![]() 为边在
为边在![]() 外作等边三角形
外作等边三角形![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,与
,与![]() 相交于点
相交于点![]() ,连接
,连接![]() .
.

(1)说明:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 是直线
是直线![]() 上的一点.则当
上的一点.则当![]() 在何处时,
在何处时,![]() 最小,并求此时
最小,并求此时![]() 的值.
的值.
【答案】(1)证明见解析;(2)点P在点E处时PB+PC最小,最小值为12cm.
【解析】
(1)根据等边三角形“三合一”的性质证得DE垂直平分AC;然后由垂直平分线的性质可得AE=CE,根据等边对等角、直角三角形的两个锐角互余的性质以及等量代换求得∠BCE=∠B;最后根据等角对等边证得CE=BE,可得AE=CE=BE;(2)由DA⊥AB可得∠BAC=30°,可求出AB的长,由(1)知,DE垂直平分AC,故PC=PA;由等量代换知PB+PC=PB+PA;根据两点之间线段最短可知,当点P、B、A在同一直线上最小,所以点P在E处时最小.
∵DF⊥AC,△ACD是等边三角形,
∴DF垂直平分AC,
∴AE=CE,
∴∠ACE=∠CAE,
∵∠ACB=90°,
∴∠ACE+∠BCE=∠CAE+∠B=90°,
∴∠BCE=∠B,
∴CE=BE,
∴AE=CE=BE;
(2)∵DA⊥AB,∠DAC=60°,
∴∠BAC=30°,
∵∠ACB=90°,BC=6,
∴AB=2BC=12,
由(1)知,DE垂直平分AC,
∴PC=PA,
∴PB+PC=PB+PA;
∴当PB+PC最小时,即PB+PA最小,
∵点P、B、A在同一直线上时,PB+PA最小,
∴点P在点E处时PB+PA最小.即PB+PC最小,
当点P在E处时,PB+PC=BE+CE=BE+AE=AB=12cm.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,抛物线y=﹣x2+bx+c过A、B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.

(1)求抛物线的解析式.
(2)求△ABE面积的最大值.
(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求出点D坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,CD⊥DA,DA⊥AB,∠1=∠2.试确定射线DF与AE的位置关系,并说明你的理由.

(1)问题的结论:DF______AE.
(2)证明思路欲证DF______AE,只要证∠3=______.
(3)证明过程:
证明:∵CD⊥DA,DA⊥AB,( )
∴∠CDA=∠DAB=______°(垂直定义)
∵∠1=∠2,( )
∴∠CDA-∠1=______-______,(等式的性质)
即∠3=______
∴DF______AE( , )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
(1)当t=2时,则AP= ,此时点P的坐标是 。
(2)当t=3时,求过点P的直线l:y=-x+b的解析式?
(3)当直线l:y=-x+b从经过点M到点N时,求此时点P向上移动多少秒?
(4)点Q在x轴时,若S△ONQ=8时,请直按写出点Q的坐标是 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,把△ABC绕AC边的中点M旋转后得△DEF,若直角顶点F恰好落在AB边上,且DE边交AB边于点G,若AC=4,BC=3,则AG的长为( )

A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求b、c的值;
(2)P为抛物线上的点,且满足S△PAB=8,求P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
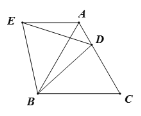
【题目】如图,在等边 ABC中,D是边AC上一点,连接BD. 将 BCD绕点B逆时针旋转60°得到 BAE,连接ED. 若BC=10,BD=9,求 AED的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com