
【题目】如图,在等边 ABC中,D是边AC上一点,连接BD. 将 BCD绕点B逆时针旋转60°得到 BAE,连接ED. 若BC=10,BD=9,求 AED的周长。
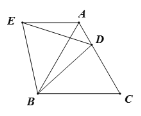
【答案】19.
【解析】
先由△ABC是等边三角形得出AC=AB=BC=10,根据图形旋转的性质得出AE=CD,BD=BE,故可得出AE+AD=AD+CD=AC=10,由∠EBD=60°,BE=BD即可判断出△BDE是等边三角形,故DE=BD=9,故△AED的周长=AE+AD+DE=AC+BD=19.
∵△ABC是等边三角形,
∴AC=AB=BC=10,
∵△BAE由△BCD逆时针旋旋转60°得出,
∴AE=CD,BD=BE,∠EBD=60°,
∴AE+AD=AD+CD=AC=10,
∵∠EBD=60°,BE=BD,
∴△BDE是等边三角形,
∴DE=BD=9,
∴△AED的周长=AE+AD+DE=AC+BD=19.
故答案为:19.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】通过计算我们知道:
(a-1)(a+1)=a2-1
(a-1)(a2+a+1)=a3-1
(a-1)(a3+a2+a+1)=a4-1
(1)请根据以上计算规律填空:(a-1)(an+an-1+…+a3+a2+a+1)=______
(2)根据上述规律,请你求出32018+32017+…+33+32+3+1的个位上的数字.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲同学手中藏有三张分别标有数字![]() 、
、![]() 、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
(1)请你用树形图或列表法列出所有可能的结果;
(2)现制定一个游戏规则:若所选出的a,b能使得ax2+bx+1=0有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请用概率知识解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,以
,以![]() 为边在
为边在![]() 外作等边三角形
外作等边三角形![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,与
,与![]() 相交于点
相交于点![]() ,连接
,连接![]() .
.

(1)说明:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 是直线
是直线![]() 上的一点.则当
上的一点.则当![]() 在何处时,
在何处时,![]() 最小,并求此时
最小,并求此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真观察图26.1的4个图中阴影部分构成的图案,回答下列问题:

(1)请写出这四个图案都具有的两个共同特征.
特征1:_________________________________________________;
特征2:_________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=mx+n的图像与x轴交于点B,与反比例函数![]() (k﹥0)的图像交于点C,过点C作CH⊥x轴,点D是反比例函数图像上的一点,直线CD与x轴交于点A,若∠HCB=∠HCA,且BC=10,BA=16.
(k﹥0)的图像交于点C,过点C作CH⊥x轴,点D是反比例函数图像上的一点,直线CD与x轴交于点A,若∠HCB=∠HCA,且BC=10,BA=16.
(1)若OA=11,求k的值;
(2)沿着x轴向右平移直线BC,若直线经过H点时恰好又经过点D,求一次函数函数y=mx+n的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的图像反映的过程是:甲乙两人同时从![]() 地出发,以各自的速度匀速向
地出发,以各自的速度匀速向![]() 地行驶,甲先到
地行驶,甲先到![]() 地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为
地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为![]() ,
, ![]() 表示甲乙两人相距的距离,
表示甲乙两人相距的距离, ![]() 表示乙行驶的时间.现有以下
表示乙行驶的时间.现有以下![]() 个结论:①
个结论:①![]() 、
、![]() 两地相距
两地相距![]() ;②点
;②点![]() 的坐标为
的坐标为![]() ;③甲去时的速度为
;③甲去时的速度为![]() ;④甲返回的速度是
;④甲返回的速度是![]() .以上
.以上![]() 个结论中正确的是_______________.
个结论中正确的是_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )

A. AE=AC B. ∠B=∠D C. BC=DE D. ∠C=∠E
查看答案和解析>>
科目:初中数学 来源: 题型:
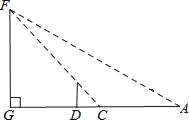
【题目】小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆GF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.
(1)若旗杆的高度FG是a米,用含a的代数式表示DG.
(2)小明从点C后退6米在A的测得旗杆顶点F的仰角为30°,求旗杆FG的高度.(点A、C、D、G在一条直线上, ![]() ,
, ![]() ,结果精确到0.1)
,结果精确到0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com