
【题目】如图,已知等腰Rt△ABC,∠ACB=90°,CA=CB,以BC为边向外作等边△CBA,连接AD,过点C作∠ACB的角平分线与AD交于点E,连接BE.

(1)若AE=2,求CE的长度;
(2)以AB为边向下作△AFB,∠AFB=60°,连接FE,求证:FA+FB= ![]() FE.
FE.
【答案】(1)![]() ﹣1;(2)证明见解析
﹣1;(2)证明见解析
【解析】试题分析:(1)延长CE交AB于G,首先判断出△CAG是等腰直角三角形,然后找到∠EAB=∠CAB﹣∠CAD=30°,分别求出CG,EG即可解决问题;
(2)延长FB到H,使得BH=AF,连接EH.作EI⊥BF于I.由△ACE≌△BCE,推出AE=BE,推出∠EAB=∠EBC=30°,由△AFE≌△BHE,推出∠AFE=∠BHE,EF=EH,可得∠EFB=∠EBH=∠AFE=30°,又EI⊥FH,故在Rt△FEI中,∠EFI=30°,从而得出FI=![]() FE,可得FA+FB=
FE,可得FA+FB=![]() FE.
FE.
试题解析:解:(1)延长CE交AB于G.
∵△BAC是等腰直角三角形,CE平分∠ACB,∴CG⊥AB,∴∠AGC=90°.
∵CA=CB,∠ACB=90°,∴∠CAB=45°,∴△CAG是等腰直角三角形.
∵△BCD是等边三角形,∴BC=CD=AC,∠BCD=60°,∴∠CAD=∠CDA,∴∠ACD=∠ACB+∠BCD=150°,∴∠CAD=∠CDA=15°,∴∠EAB=∠CAB﹣∠CAD=30°.
在Rt△AEG中,∠EAG=30°,AE=2,∴AE=![]() ,EG=1.
,EG=1.
∵CG=AG=![]() ,∴CE=CG﹣EG=
,∴CE=CG﹣EG=![]() ﹣1.
﹣1.
(2)延长FB到H,使得BH=AF,连接EH.作EI⊥BF于I.
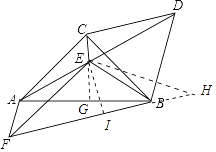
由(1)可知:AC=BC,CE平分∠ACB,∴∠ACE=∠BCE.
∵CE=CE,∴△ACE≌△BCE,∴AE=BE,∴∠EAB=∠EBC=30°.
在△AFB中,∠AFB=60°,∴∠FAB+∠FBA=120°,∴∠FAE=∠EAB+∠FAB=30°+∠FAB,∠EBH=180°﹣∠EBA﹣∠ABF=150°﹣(120°﹣∠ABF)=30°+∠FAB,∴∠EBH=∠FAE,∴△AFE≌△BHE,∴∠AFE=∠BHE,EF=EH,∴∠EFB=∠EBH=∠AFE=30°.
∵EI⊥FH,∴EI=IH,在Rt△FEI中,∠EFI=30°,∴FI= ![]() FE,∴FH=BH+FB=
FE,∴FH=BH+FB=![]() FE,∴FA+FB=
FE,∴FA+FB=![]() FE.
FE.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】某市2013年启动省级园林城市创建工作,计划2015年下半年顺利通过验收评审.该市为加快道路绿化及防护绿地等各项建设.在城市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发匀速相向而行,大楼C位于AB之间,甲与乙相遇在AC中点处,然后两车立即掉头,以原速原路返回,直到各自回到出发点.设甲、乙两车距大楼C的距离之和为y(千米),甲车离开A地的时间为t(小时),y与t的函数图象所示,则第21小时时,甲乙两车之间的距离为________千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月16日,第十五届文博会在深圳拉开帷幕,周末,小明骑共享单车从家里出发去分会馆参观,途中突然发现钥匙不见了,于是原路折返,在刚才等红绿灯的路口找到了钥匙,便继续前往分会馆,设小明从家里出发到分会场所用的时间为x(分钟),离家的距离为y(米),且x与y的关系示意图如图所示,请根据图中提供的信息回答下列问题:
(1)图中自变量是 .因变量是 .
(2)小明等待红绿灯花了 分钟.
(3)小明的家距离分会馆 米
(4)小明在 时间段的骑行速度最快,最快速度是 米/分钟.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任意写出一个数位不含零的三位数,任取三个数字中的两个,组合成所有可能的两位数(有6个),求出所有这些两位数的和,然后将它除以原三位数的各个数位上的数的和.例如,对三位数223,取其两个数字组成所有可能的两位数:22,23,22,23,32,32.它们的和是154.三位数223各位数的和是7,![]() 再换几个数试一试,你发现了什么?请写出你按上面方法的探索过程和所发现的结果,并运用代数式的知识说明所发现的结果的正确性.
再换几个数试一试,你发现了什么?请写出你按上面方法的探索过程和所发现的结果,并运用代数式的知识说明所发现的结果的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“阅读素养的培养是构建核心素养的重要基础,重庆十一中学校以‘大阅读’特色课程实施为突破口,着力提升学生的核心素养.”全校师生积极响应和配合,开展各种活动丰富其课余生活.在数学兴趣小组中,同学们从书上认识了很多有趣的数.其中有一个“和平数”引起了同学们的兴趣.描述如下:一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果![]() ,那么称这个四位数为“和平数”.
,那么称这个四位数为“和平数”.
例如:1423,![]() ,
,![]() ,因为
,因为![]() ,所以1423是“和平数”.
,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是________,最大的“和平数”是__________;
(2)求同时满足下列条件的所有“和平数”:
①个位上的数字是千位上的数字的两倍;
②百位上的数字与十位上的数字之和是12的倍数;
(3)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后这两个“和平数”为“相关和平数”.
例如:1423于4132为“相关和平数”
求证:任意的两个“相关和平数”之和是1111的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
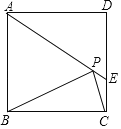
【题目】如图,在正方形ABCD中,AD=2![]() ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.
,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知点A、B是反比例函数y=﹣![]() 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校书法兴趣小组准备到文具店购买A、B两种类型的毛笔,文具店的销售方法是:一次性购买A型毛笔不超过20支时,按零售价销售;超过20支时,超过部分每支比零售价低0.4元,其余部分仍按零售价销售.一次性购买B型毛笔不超过15支时,按零售价销售;超过15支时,超过部分每支比零售价低0.6元,其余的部分仍按零售价销售.
(1)如果全组共有20名同学,若每人各买1支A型毛笔和2支B型毛笔,共支付145元;若每人各买2支A型毛笔和1支B型毛笔,共支付129元,这家文具店的A、B型毛笔的零售价各是多少?
(2)为了促销,该文具店对A型毛笔除了原来的销售方法外,同时又推出了一种新的销售方法:无论购买多少支,一律按原零售价(即(1)中所求得的A型毛笔的零售价)90%出售.现要购买A型毛笔a支(a>40),在新的销售方法和原来的销售方法中,应选择哪种方法购买花钱较少并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com