
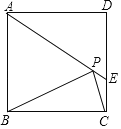
【题目】如图,在正方形ABCD中,AD=2![]() ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.
,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.
【答案】9﹣5![]()
【解析】
根据旋转的想知道的PB=BC=AB,∠PBC=30°,推出△ABP是等边三角形,得到∠BAP=60°,AP=AB=2![]() ,解直角三角形得到CE=2
,解直角三角形得到CE=2![]() -2,PE=4-2
-2,PE=4-2![]() ,过P作PF⊥CD于F,于是得到结论.
,过P作PF⊥CD于F,于是得到结论.
∵四边形ABCD是正方形,∴∠ABC=90°,∵把边BC绕点B逆时针旋转30°得到线段BP,∴PB=BC=AB,∠PBC=30°,∴∠ABP=60°,∴△ABP是等边三角形,∴∠BAP=60°,AP=AB=2![]() ,∵AD=2
,∵AD=2![]() ,∴AE=4,DE=2,∴CE=2
,∴AE=4,DE=2,∴CE=2![]() ﹣2,PE=4﹣2
﹣2,PE=4﹣2![]() ,过P作PF⊥CD于F,∴PF=
,过P作PF⊥CD于F,∴PF=![]() PE=2
PE=2![]() ﹣3,∴三角形PCE的面积=
﹣3,∴三角形PCE的面积=![]() CEPF=
CEPF=![]() ×(2
×(2![]() ﹣2)×(2
﹣2)×(2![]() ﹣3)=9-5
﹣3)=9-5![]() ,故答案为:9-5
,故答案为:9-5![]() .
.


科目:初中数学 来源: 题型:
【题目】(1) [探索发现]正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一个动点(与点
上的一个动点(与点![]() 不重合),过点
不重合),过点![]() 作
作![]() 交线段
交线段![]() 于点
于点![]() .求证:
.求证: ![]()
小玲想到的思路是:过点![]() 作
作![]() 于点
于点![]() 于点
于点![]() ,通过证明
,通过证明![]() 得到
得到![]() .请按小玲的思路写出证明过程
.请按小玲的思路写出证明过程

(2)[应用拓展]如图2,在![]() 的条件下,设正方形
的条件下,设正方形![]() 的边长为
的边长为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .求
.求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰Rt△ABC,∠ACB=90°,CA=CB,以BC为边向外作等边△CBA,连接AD,过点C作∠ACB的角平分线与AD交于点E,连接BE.

(1)若AE=2,求CE的长度;
(2)以AB为边向下作△AFB,∠AFB=60°,连接FE,求证:FA+FB= ![]() FE.
FE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:ABC平移后得出△A1B1C1,点A(﹣1,3)平移后得A1(﹣4,2),又已知B1(﹣2,3),C1(1,﹣1),求B、C坐标,画图并说明经过了怎样的平移.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON.
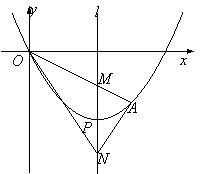
(1)求该二次函数的关系式;
(2)若点A的坐标是(6,-3),求△ANO的面积;
(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夏季的一天,身高为1.6m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为( )

A.8m B.6.4m C.4.8m D.10m
【答案】A.
【解析】
试题分析:因为人和树均垂直于地面,所以和光线构成的两个直角三角形相似,
设树高x米,则![]() ,即
,即![]() ,解得,x=8. 故选A.
,解得,x=8. 故选A.
考点:相似三角形的应用.
【题型】单选题
【结束】
11
【题目】已知圆锥的底面半径为1cm,母线长为3cm,则其全面积为________cm2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
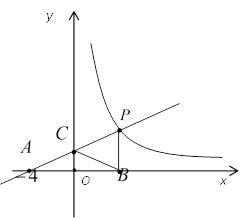
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() 垂直
垂直![]() 轴于点
轴于点![]() ,且
,且![]() .
.
(1)仔细观察图形,直接写出![]() ;
;
(2)求![]() 和
和![]() 的值;
的值;
(3)在反比例函数图象上是否存在点![]() ,使四边形
,使四边形![]() 为平行四边形,如果存在,求出点
为平行四边形,如果存在,求出点![]() 的坐标,如果不存在,请说明理由.
的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:

根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在抽样数据中,产生的有害垃圾共 吨;
(3)调查发现,在可回收物中塑料类垃圾占![]() ,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com