
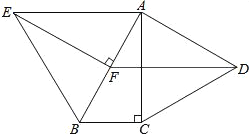
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知∠ABC=60°,EF⊥AB,垂足为F,连接DF.
(1)求证:△ABC≌△EAF;
(2)试判断四边形EFDA的形状,并证明你的结论.
【答案】(1)证明见解析(2)四边形EFDA是平行四边形
【解析】试题分析:(1)首先Rt△ABC中,由∠BAC=30°可以得到AB=2BC,又因为△ABE是等边三角形,EF⊥AB,由此得到AE=2AF,并且AB=2AF,然后即可证明△AFE≌△BCA,再根据全等三角形的性质即可证明AC=EF;
(2)根据(1)知道EF=AC,而△ACD是等边三角形,所以EF=AC=AD,并且AD⊥AB,而EF⊥AB,由此得到EF∥AD,再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形.
试题解析:(1)∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,
∴AB=2AF
∴AF=BC,
在Rt△AFE和Rt△BCA中,
![]() ,
,
∴△AFE≌△BCA(HL),
∴AC=EF;
(2)∵△ACD是等边三角形,
∴∠DAC=60°,AC=AD,
∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB,
∴EF∥AD,
∵AC=EF,AC=AD,
∴EF=AD,
∴四边形ADFE是平行四边形.


科目:初中数学 来源: 题型:
【题目】已知M(1,﹣2),N(﹣3,﹣2),则直线MN与x轴,y轴的位置关系分别为( )
A.相交,相交
B.平行,平行
C.垂直相交,平行
D.平行,垂直相交
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(x-3)2图像上的两个不同的点A(3,a)和B(x,b),则a和b的大小关系( )
A. a≤bB. a>bC. a<bD. a≥b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现:小琼步行![]() 步与小刚步行
步与小刚步行![]() 步消耗的能量相同,若每消耗
步消耗的能量相同,若每消耗![]() 千卡能量小琼行走的步数比小刚多
千卡能量小琼行走的步数比小刚多![]() 步,求小刚每消耗
步,求小刚每消耗![]() 千卡能量需要行走多少步?
千卡能量需要行走多少步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.

(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心,支架CD与水平面AE垂直,AB=110厘米,∠BAC=37°,垂直支架CD=57厘米,DE是另一根辅助支架,且∠CED=60°.
(1)求辅助支架DE长度;(结果保留根号)
(2)求水箱半径OD的长度.(结果精确到1厘米,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com