
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.

(1)探究:线段OE与OF的数量关系并加以证明;
(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明;若不是,则说明理由;
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
【答案】(1)OE=OF.(2)四边形BCFE不可能是菱形(3)当点O为AC中点且△ABC是以∠ACB为直角三角形时,四边形AECF是正方形.
【解析】
试题分析:(1)利用平行线的性质由角相等得出边相等;
(2)假设四边形BCFE,再证明与在同一平面内过同一点有且只有一条直线与已知直线垂直相矛盾;
(3)利用平行四边形及等腰直角三角形的性质证明四边形AECF是正方形.
解:(1)OE=OF.
证明如下:
∵CE是∠ACB的平分线,
∴∠1=∠2.
∵MN∥BC,
∴∠1=∠3.
∴∠2=∠3.
∴OE=OC.
同理可证OC=OF.
∴OE=OF.(3分)
(2)四边形BCFE不可能是菱形,若四边形BCFE为菱形,则BF⊥EC,
而由(1)可知FC⊥EC,在平面内过同一点F不可能有两条直线同垂直于一条直线.(3分)
(3)当点O运动到AC中点时,且△ABC是直角三角形(∠ACB=90°)时,四边形AECF是正方形.
理由如下:
∵O为AC中点,
∴OA=OC,
∵由(1)知OE=OF,
∴四边形AECF为平行四边形;
∵∠1=∠2,∠4=∠5,∠1+∠2+∠4+∠5=180°,
∴∠2+∠5=90°,即∠ECF=90°,
∴AECF为矩形,
又∵AC⊥EF.
∴AECF是正方形.
∴当点O为AC中点且△ABC是以∠ACB为直角三角形时,四边形AECF是正方形.(3分)



科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,以AB为直角边作等腰直角三角形ABD,与BC边交于点E,
(1)若∠ACE=18°,则∠ECD=
(2)探索:∠ACE与∠ACD有怎样的数量关系?猜想并证明.
(3)如图2,作△ABC的高AF并延长,交BD于点G,交CD延长线于点H,求证:CH2+DH2=2AD2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一大重要研究成果.如图所示的三角形数表,称“杨辉三角”.具体法则:两侧的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律:
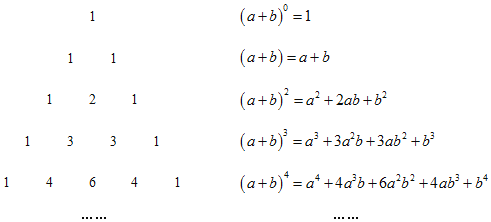
(1)根据上面的规律,写出(a+b)5的展开式;
(2)利用上面的规律计算:(﹣3)4+4×(﹣3)3×2+6×(﹣3)2×22+4×(﹣3)×23+24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次考试中,某班级的数学成绩统计图如图.下列说法错误的是( )

A. 得分在70~80分之间的人数最多 B. 该班的总人数为40
C. 得分在90~100分之间的人数最少 D. 及格(≥60分)人数是26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD,AE分别是△ABC的高和中线,AB=3cm,AC=4cm,BC=5cm,∠CAB=90°,求:
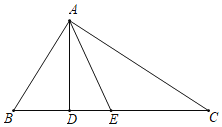
(1)AD的长;
(2)△ACE和△ABE的周长的差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.
(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com