
【题目】如图1,在△ABC中,AB=AC,以AB为直角边作等腰直角三角形ABD,与BC边交于点E,
(1)若∠ACE=18°,则∠ECD=
(2)探索:∠ACE与∠ACD有怎样的数量关系?猜想并证明.
(3)如图2,作△ABC的高AF并延长,交BD于点G,交CD延长线于点H,求证:CH2+DH2=2AD2.

【答案】(1)45°;(2)∠ACE=∠ACD﹣45°,理由见解析;(2)见解析
【解析】
(1)由等腰三角形的性质得出∠ABC=∠ACE=18°,得出∠BAC=180°﹣18°﹣18°=144°,由等腰直角三角形的性质得出∠BAD=90°,AB=AD,求出∠DAC=54°,证出AC=AD,由等腰三角形的性质和三角形内角和定理得出∠ACD=![]() (180°﹣54°)=63°,即可得出答案;
(180°﹣54°)=63°,即可得出答案;
(2)由(1)得出∠BAC=180°﹣2∠ACE,得出∠DAC=90°﹣2∠ACE,由等腰三角形的性质和三角形内角和定理即可得出结论;
(3)连接BH,由(2)得出∠ECD=45°,由等腰三角形的性质得出BF=CF,由线段垂直平分线的性质得出BH=CH,由等腰三角形的性质得出∠HBC=∠BCD=45°,证出∠BHC=90°,由勾股定理得出BH2+DH2=BD2.进而得出结论.
(1)∵AB=AC,
∴∠ABC=∠ACE=18°,
∴∠BAC=180°﹣18°﹣18°=144°,
∵以AB为直角边作等腰直角三角形ABD,
∴∠BAD=90°,AB=AD,
∴∠DAC=144°﹣90°=54°,
∵AB=AC,
∴AC=AD,
∴∠ACD=![]() (180°﹣54°)=63°,
(180°﹣54°)=63°,
∴∠DCE=∠ACD﹣∠ACE=63°﹣18°=45°;
故答案为:45°;
(2)∠ACE=∠ACD﹣45°;理由如下:
由(1)得:∠BAC=180°﹣2∠ACE,
∴∠DAC=∠BAC﹣90°=90°﹣2∠ACE,
∵AC=AD,
∴∠ACD=![]() (180°﹣∠DAC)=
(180°﹣∠DAC)=![]() [180°﹣(90°﹣2∠ACE)]=45°+∠ACE,
[180°﹣(90°﹣2∠ACE)]=45°+∠ACE,
∴∠ACE=∠ACD﹣45°;
(3)连接BH,如图2所示:
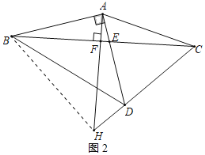
由(2)得:∠ECD=45°,
∵AB=AC,AF⊥BC,
∴BF=CF,
∴BH=CH,
∴∠HBC=∠BCD=45°,
∴∠BHC=90°,
∴BH2+DH2=BD2.
∵△ABD是等腰直角三角形,
∴BD2=2AD2,
∴CH2+DH2=2AD2.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】推理填空:
如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2= .( )
又因为∠1=∠2,
所以∠1=∠3.( )
所以AB∥ .( )
所以∠BAC+ =180°( )
又因为∠BAC=70°,
所以∠AGD= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是( )

A. 504m2 B. ![]() m2 C.
m2 C. ![]() m2 D. 1009m2
m2 D. 1009m2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系(每格的宽度为1)中,已知点A的坐标是![]() ,点B的坐标是
,点B的坐标是![]() ,
,

![]()
(1)在直角坐标平面中画出线段AB;
(2)B点到原点O的距离是 ;
(3)将线段AB沿![]() 轴的正方向平移4个单位,画出平移后的线段A1BI,并写出点A1、B1的坐标.
轴的正方向平移4个单位,画出平移后的线段A1BI,并写出点A1、B1的坐标.
(4)求△A1B B1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: ![]() .
.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.

(1)探究:线段OE与OF的数量关系并加以证明;
(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明;若不是,则说明理由;
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com