
����Ŀ����ABC�͡�ADE�У�AB=AC��AD=AE����BAC=��DAE=����0�㣼����90�㣩����F��G��P�ֱ���DE��BC��CD���е㣬����PF��PG��
��1����ͼ�٣���=90�㣬��D��AB�ϣ����FPG= �㣻
��2����ͼ�ڣ���=60�㣬��D����AB�ϣ��жϡ�FPG�Ķ�������֤����Ľ��ۣ�
��3������FG����AB=5��AD=2���̶���ABC������ADE�Ƶ�A��ת����PF���ȵ����ֵΪ ��PF���ȵ���СֵΪ ��



��27��
���𰸡���1����GPF=90�㣻��2������FPG=120�㣬���������������3��![]() ��
��![]()
��������
��1����AB=AC��AD=AE���ó�BD=CE���ٸ���G��P��F�ֱ���BC��CD��DE���ص㣬���Եó�PG��BD,PF��CE.���GPF=180��-����=90��
(2)����BD��CE,����֪����֤����ABD�ա�ACE,���ABD=��ACE,��ΪG��P��F�ֱ���BC��CD��DE���е㣬��PG��BD,PF��CE,�����ó���GPF=180��-����=120��.
��3����D��BA���ӳ�����ʱ��CE=BD�����ʱBD=AB+AD=7;
��1����AB=AC��AD=AE��
��BD=CE��
��G��P��F�ֱ���BC��CD��DE���е㣬
��PG��BD��PF��CE��
���ADC=��DPG����DPF=��ACD��
���GPF=��DPF+��DPG=��ADC+��ACD=180��-��BAC=180��-����=90�㣬
����GPF=90�㣻
��2����FPG=120�����������£�

����BD������CE����ͼ��
�ߡ�BAC=��DAE��
���BAD=��CAE������ABD����ACE��

���ABD�ա�ACE��SAS����
���ABD=��ACE��
��G��P��F�ֱ���BC��CD��DE���е㣬
��PG��BD��PF��CE��
���PGC=��CBD����DPF=��DCE=��DCA+��ACE=��DCA+��ABD����DPG=��PGC+��BCD=��CBD+��BCD��
���GPF=��DPF+��DPG=��DCA+��ABD+��CBD+��BCD=180��-��BAC=180��-����=120�㣬
����GPF=120�㣻
��3��![]() ��
��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼΪ���κ���y=ax2+bx+c��a��0����ͼ��������˵������a��0 ��2a+b=0 ��a+b+c��0 �ܵ���1��x��3ʱ��y��0��������ȷ�ĸ���Ϊ��������

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ϊ2����Ϊ1�ľ���ABCD�;���EFGH��ͼ1��ʾ�ڷ���ֱ��l�ϣ�DE=2��������ABCD�Ƶ�D˳ʱ����ת���ǣ�0�㣼����90������������EFGH�Ƶ�E��ʱ����ת��ͬ�ĽǶȣ�����ת�Ĺ����У�����ͼ2˼����������ABCD�;���EFGH�غϲ���Ϊ������ʱ����=_____�㣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ��������ֽƬ![]() ��ͼ��
��ͼ��![]() ������
������![]() ��ֽƬ�ع���B��ֱ���۵���ʹ��C�䵽AB���ϵ�E�㴦���ۺ�Ϊ
��ֽƬ�ع���B��ֱ���۵���ʹ��C�䵽AB���ϵ�E�㴦���ۺ�Ϊ![]() ��ͼ��
��ͼ��![]() �ٽ�ֽƬ�ع���E��ֱ���۵�����Aǡ�����D�غϣ��ۺ�Ϊ
�ٽ�ֽƬ�ع���E��ֱ���۵�����Aǡ�����D�غϣ��ۺ�Ϊ![]() ��ͼ��
��ͼ��![]() ԭ������ֽƬABC�У�
ԭ������ֽƬABC�У�![]() �Ĵ�СΪ______
�Ĵ�СΪ______![]()

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��ͼ����ͼ��ʾ���������н��ۣ���
��ͼ����ͼ��ʾ���������н��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() �������н�����ȷ���ǣ� ��
�������н�����ȷ���ǣ� ��

A. �٢� B. �ۢ� C. �ڢ� D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ƽ���ı���ABCD�У�BC=3��AB=4��![]() ��EΪ�߶�BC������һ�㣬����AE���ӳ���DC���ڵ�G����BE=2EC����AE�ı߳�Ϊ�� ��
��EΪ�߶�BC������һ�㣬����AE���ӳ���DC���ڵ�G����BE=2EC����AE�ı߳�Ϊ�� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
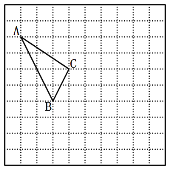
����Ŀ������ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊ1����������Σ������������ߵĽ���������Σ�,��ABC�Ķ���A��B������ֱ�Ϊ������4��3������-2����1����
��1������ͼ������ƽ��ֱ������ϵ��д����C�����ꣻ
��2������������ABC����ƽ��2����λ���ȣ�������ƽ��3����λ���Ⱥ��![]() ����д����C�������꣮
����д����C�������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������C�ڡ�O�ϣ�����C������CM�������ACM=��ABC��
��1���ж�CM���O��λ�ù�ϵ����֤����
��2���ӳ�BC��D��ʹBC=CD������AD��CM���ڵ�E������O�İ뾶Ϊ3��ED=2������ACE�����Բ�İ뾶��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com