
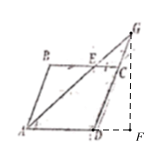
【题目】如图,已知在平行四边形ABCD中,BC=3,AB=4,![]() ,E为线段BC上任意一点,连接AE并延长与DC交于点G,若BE=2EC,则AE的边长为( )
,E为线段BC上任意一点,连接AE并延长与DC交于点G,若BE=2EC,则AE的边长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
过G 作GF垂直AD的延长线于F,根据平行四边形的性质可知△ABE∽△ECG,由BE=2EC,可知AB=2CG,AE=2GE,可求出CG的长,进而求出DG的长,由∠BAD=60°,可知∠GDF=60°,根据∠GDF的三角函数可求出DF、GF的长,根据勾股定理可求出AG的长,进而求出AE的长即可
∵ABCD是平行四边形,
∴易得△ABE∽△ECG,
∵BE=2EC,
∴AB=2CG,AE=2GE,
∴CG=2,DG=6,
∵∠GDF=∠BAD=60°,
∴DF=DG![]() cos60°=3,AF=6,GF=DG
cos60°=3,AF=6,GF=DG![]() sin60°=3
sin60°=3![]() ,
,
∴根据勾股定理AG2=AF2+GF2=36+27=63,
∴AG=3![]() ,
,
∴AE=![]() AG=
AG=![]() ,
,
故选A.


科目:初中数学 来源: 题型:
【题目】某工厂修建了甲、乙两个水池,最大蓄水量都是1200立方米,如果甲池有水480立方米,乙池蓄满水,甲池每小时进水80立方米,乙池每小时放水100立方米.
(1)分别写出甲、乙两池的水量![]() 与时间
与时间![]() 的函数解析式;
的函数解析式;
(2)甲、乙两池同时进水、放水,经过几小时两个水池内的水一样多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
(1)当t=2时,则AP= ,此时点P的坐标是 。
(2)当t=3时,求过点P的直线l:y=-x+b的解析式?
(3)当直线l:y=-x+b从经过点M到点N时,求此时点P向上移动多少秒?
(4)点Q在x轴时,若S△ONQ=8时,请直按写出点Q的坐标是 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=α(0°<α≤90°),点F,G,P分别是DE,BC,CD的中点,连接PF,PG.
(1)如图①,α=90°,点D在AB上,则∠FPG= °;
(2)如图②,α=60°,点D不在AB上,判断∠FPG的度数,并证明你的结论;
(3)连接FG,若AB=5,AD=2,固定△ABC,将△ADE绕点A旋转,则PF长度的最大值为 ;PF长度的最小值为 ;



第27题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 图象
图象![]() 轴上方的部分沿
轴上方的部分沿![]() 轴翻折到
轴翻折到![]() 轴下方,图象的其余部分保持不变,翻折后的图象与原图象
轴下方,图象的其余部分保持不变,翻折后的图象与原图象![]() 轴下方的部分组成一个“
轴下方的部分组成一个“![]() ”形状的新图象,若直线
”形状的新图象,若直线![]() 与该新图象有两个公共点,则
与该新图象有两个公共点,则![]() 的取值范围为_____.
的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD//BC,![]() ,
,![]() ,
,![]() ,
,![]() ,动点M从B点出发沿线段BC以每秒2个单位长度的速度向C运动;动点N同时从A点出发沿线段AB以每秒1个单位长度的速度向B运动,其中一点到达终点时,则两点同时停止运动.设运动的时间为t秒,当△MNB为等腰直角三角形时,t的值是_______.
,动点M从B点出发沿线段BC以每秒2个单位长度的速度向C运动;动点N同时从A点出发沿线段AB以每秒1个单位长度的速度向B运动,其中一点到达终点时,则两点同时停止运动.设运动的时间为t秒,当△MNB为等腰直角三角形时,t的值是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M为抛物线![]() 与x轴的焦点为A(-3,0),B(1,0),与y轴交于点C,连结AM,AC,点D为线段AM上一动点(不与A重合),以CD为斜边在CD上侧作等腰Rt△DEC,连结AE,OE.
与x轴的焦点为A(-3,0),B(1,0),与y轴交于点C,连结AM,AC,点D为线段AM上一动点(不与A重合),以CD为斜边在CD上侧作等腰Rt△DEC,连结AE,OE.
(1)求抛物线的解析式及顶点M的坐标;
(2)求解AD:OE的值;
(3)当△OEC为直角三角形时,求AD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月,某县突降暴雨,造成山体滑坡,桥梁垮塌,房屋大面积受损,该省民政厅急需将一批帐篷送往灾区.现有甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20件帐篷,且甲种货车装运1 000件帐篷与乙种货车装运800件帐篷所用车辆相等.
(1)求甲、乙两种货车每辆车可装多少件帐篷;
(2)如果这批帐篷有1 490件,用甲、乙两种汽车共16辆装运,甲种车辆刚好装满,乙种车辆最后一辆只装了50件,其余装满,求甲、乙两种货车各有多少辆.
查看答案和解析>>
科目:初中数学 来源: 题型:
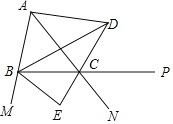
【题目】如图,∠ABC=∠ACB,BD、CD、BE分别平分△ABC的内角∠ABC、外角∠ACP、外角∠MBC,以下结论:①AD∥BC;②DB⊥BE;③∠BDC+∠ABC=90°;④∠A+2∠BEC=180°.其中正确的结论有_____.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com