
【题目】天水某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两行环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元,
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客量总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
【答案】(1)购买A型公交车每辆需100万元,购买B型公交车每辆需150万元.(2)购买A型公交车8辆,则B型公交车2辆费用最少,最少总费用为1100万元.
【解析】
(1)设购买A型公交车每辆需x万元,购买B型公交车每辆需y万元,根据“A型公交车1辆,B型公交车2辆,共需400万元;A型公交车2辆,B型公交车1辆,共需350万元”列出方程组解决问题;
(2)设购买A型公交车a辆,则B型公交车(10-a)辆,由“购买A型和B型公交车的总费用不超过1220万元”和“10辆公交车在该线路的年均载客总和不少于650万人次”列出不等式组探讨得出答案即可.
(1)设购买A型公交车每辆需x万元,购买B型公交车每辆需y万元,由题意得
![]() ,
,
解得![]() ,
,
答:购买A型公交车每辆需100万元,购买B型公交车每辆需150万元.
(2)设购买A型公交车a辆,则B型公交车(10﹣a)辆,由题意得
![]() ,
,
解得:![]() ,
,
因为a是整数,
所以a=6,7,8;
则(10﹣a)=4,3,2;
三种方案:
①购买A型公交车6辆,则B型公交车4辆:100×6+150×4=1200万元;
②购买A型公交车7辆,则B型公交车3辆:100×7+150×3=1150万元;
③购买A型公交车8辆,则B型公交车2辆:100×8+150×2=1100万元;
购买A型公交车8辆,则B型公交车2辆费用最少,最少总费用为1100万元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
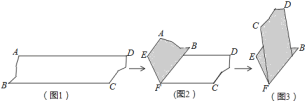
A.120°B.108°C.126°D.114°
查看答案和解析>>
科目:初中数学 来源: 题型:
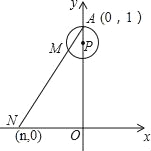
【题目】如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1.点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1).
(1)当m=![]() 时,n=_____;
时,n=_____;
(2)随着点M的转动,当m从![]() 变化到
变化到![]() 时,点N相应移动的路径长为_____.
时,点N相应移动的路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
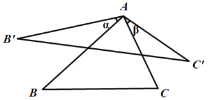
【题目】如图,将△ABC的边AB绕着点A顺时针旋转![]() (
(![]() )得到AB′,边AC绕着点A逆时针旋转
)得到AB′,边AC绕着点A逆时针旋转![]() (
(![]() )得到AC′,联结B′C′,当
)得到AC′,联结B′C′,当![]() +
+![]() =60°时,我们称
=60°时,我们称![]() AB′C′是
AB′C′是![]() ABC的“双旋三角形”,如果等边
ABC的“双旋三角形”,如果等边![]() ABC的边长为a, 那么它所得的“双旋三角形”中B′C′=___________(用含a的代数式表示).
ABC的边长为a, 那么它所得的“双旋三角形”中B′C′=___________(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人;已知36座客车每辆租金400元,42座客车每辆租金440元.
(1)该校七年级共有多少人参加春游?
(2)请你帮该校设计一种最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学为调查某小学六个年级学生每周的零花钱情况,他在学校中随机抽取了400名学生进行调查统计并制成如下图表,
|
|
请根据图表提供的信息解答下列问题:
(1)a =__________,b =__________;
(2)补全频数分布直方图;
(3)若全校共有3000名学生,请你估计该校每周零花钱超过50元的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题的提出:
如果点P是锐角△ABC内一动点,如何确定一个位置,使点P到△ABC的三顶点的距离之和PA+PB+PC的值为最小?
问题的转化:
(1)把ΔAPC绕点A逆时针旋转60度得到![]() 连接
连接![]() 这样就把确定PA+PB+PC的最小值的问题转化成确定
这样就把确定PA+PB+PC的最小值的问题转化成确定![]() 的最小值的问题了,请你利用如图证明:
的最小值的问题了,请你利用如图证明:
![]() ;
;
问题的解决:
(2)当点P到锐角△ABC的三项点的距离之和PA+PB+PC的值为最小时,请你用一定的数量关系刻画此时的点P的位置:_____________________________;
问题的延伸:
(3)如图是有一个锐角为30°的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与x轴、y轴交于
分别与x轴、y轴交于![]() 两点,与直线
两点,与直线![]() 交于点C(4,2).
交于点C(4,2).
(1)点A坐标为( , ),B为( , );
(2)在线段![]() 上有一点E,过点E作y轴的平行线交直线
上有一点E,过点E作y轴的平行线交直线![]() 于点F,设点E的横坐标为m,当m为何值时,四边形
于点F,设点E的横坐标为m,当m为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得![]() 四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com