
【题目】某小型工厂9月份生产的A、B两种产品数量分别为200件和100件,A、B两种产品出厂单价之比为2:1,由于订单的增加,工厂提高了A、B两种产品的生产数量和出厂单价,10月份A产品生产数量的增长率和A产品出厂单价的增长率相等,B产品生产数量的增长率是A产品生产数量的增长率的一半,B产品出厂单价的增长率是A产品出厂单价的增长率的2倍.设B产品生产数量的增长率为x(x>0).
(1)用含有x的代数式填表(不需化简):
9月份生产数量 | 生产数量的增长率 | 10月份生产数量 | |
产品A | 200 |
|
|
产品B | 100 | x |
|
(2)若9月份两种产品出厂单价的和为90元,10月份该工厂的总收入增加了4.4x,求x的值.
【答案】(1)2x;200(1+2x);100(1+x);(2)![]()
【解析】
(1)根据“10月份A产品生产数量的增长率和A产品出厂单价的增长率相等,B产品生产数量的增长率是A产品生产数量的增长率的一半,B产品出厂单价的增长率是A产品出厂单价的增长率的2倍”填空;
(2)根据(1)中相关量间的关系和9月份两种产品出厂单价的和为90元列出方程并解答.
(1)由题意,得:

故答案为:2x;200(1+2x);100(1+x);
(2)90×![]() =60(元),90×
=60(元),90×![]() =30(元)
=30(元)
60×200(1+2x)2+30×100(1+x)(1+4x)=(60×200+30×100)(1+4.4x)
解得:x1=0(舍去),x2=![]() .
.
即x的值是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD 的边长为 8,E 是 BC 边的中点,点 P 在射线 AD 上, 过 P 作 PF⊥AE 于 F.
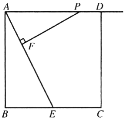
(1)请判断△PFA 与△ABE 是否相似,并说明理由;
(2)当点 P 在射线 AD 上运动时,设 PA=x,是否存在实数 x,使以 P,F,E 为顶 点的三角形也与△ABE 相似?若存在,请求出 x 的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个同学做了一个数字游戏:拿出三张正面写有数字![]() ,2,3且背面完全相同的卡片,将这三张卡片背面朝上洗匀后,甲先随机抽取一张,将所得数字作为
,2,3且背面完全相同的卡片,将这三张卡片背面朝上洗匀后,甲先随机抽取一张,将所得数字作为![]() 的值,然后将卡片放回并洗匀,乙再从这三张卡片中随机抽取一张,将所得数字作为
的值,然后将卡片放回并洗匀,乙再从这三张卡片中随机抽取一张,将所得数字作为![]() 的值,两次结果记为
的值,两次结果记为![]() .
.
(1)请你帮他们用画树状图或列表的方法表示![]() 所有可能出现的结果;
所有可能出现的结果;
(2)若将记录结果![]() 看成平面直角坐标系中的一点,求
看成平面直角坐标系中的一点,求![]() 是第一象限内的点的概率.
是第一象限内的点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新能源汽车投放市场后,有效改善了城市空气质量。经过市场调查得知,某市去年新能源汽车总量已达到3250辆,预计明年会增长到6370辆.
(1)求今、明两年新能源汽车数量的平均增长率;
(2)为鼓励市民购买新能源汽车,该市财政部门决定对今年增加的新能源汽车给予每辆0.8万元的政府性补贴.在(1)的条件下,求该市财政部门今年需要准备多少补贴资金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年9月,我国中小学生迎来了新版“教育部统编义务教育语文教科书”,本次“统编本”教材最引人关注的变化之一是强调对传统文化经典著作的阅读,某校对A《三国演义》、B《红楼梦》、C《西游记》、D《水浒》四大名著开展“最受欢迎的传统文化经典著作”调查,随机调查了若干名学生(每名学生必选且只能选这四大名著中的一部)并将得到的信息绘制了下面两幅不完整的统计图:

(1)本次一共调查了 名学生;
(2)请将条形统计图补充完整;
(3)某班语文老师想从这四大名著中随机选取两部作为学生暑期必读书籍,请用树状图或列表的方法求恰好选中《三国演义》和《红楼梦》的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的自变量x与函数值y的对应值如图,下列说法错误的是:( )
x | … | ﹣6 | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | … |
y | … | 10 | 4 | 0 | ﹣2 | ﹣2 | 0 | … |
A.抛物线开口向上
B.抛物线与y轴的交点是(0,4)
C.当x<﹣2时,y随x的增大而减小
D.当x>﹣2时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学以致用:问题1:怎样用长为![]() 的铁丝围成一个面积最大的矩形?
的铁丝围成一个面积最大的矩形?
小学时我们就知道结论:围成正方形时面积最大,即围成边长为![]() 的正方形时面积最大为
的正方形时面积最大为![]() .请用你所学的二次函数的知识解释原因.
.请用你所学的二次函数的知识解释原因.
思考验证:问题2:怎样用铁丝围一个面积为![]() 且周长最小的矩形?
且周长最小的矩形?
小明猜测:围成正方形时周长最小.
为了说明其中的道理,小明翻阅书籍,找到下面的材料:
结论:在![]() 、
、![]() 均为正实数)中,若
均为正实数)中,若![]() 为定值
为定值![]() ,则
,则![]() ,当且仅当
,当且仅当![]() 时,
时,![]() 有最小值
有最小值![]() .
.
![]()
![]() 均为正实数)的证明过程:
均为正实数)的证明过程:
对于任意正实数![]() 、
、![]() ,
,![]()
![]() ,
,![]()
![]() ,
,
![]()
![]() ,当且仅当
,当且仅当![]() 时,等号成立。
时,等号成立。
解决问题:
(1)若![]() ,则
,则![]() (当且仅当
(当且仅当![]() 时取“
时取“![]() ”
” ![]() ;
;
(2)运用上述结论证明小明对问题2的猜测;
(3)当![]() 时,求
时,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com