
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD. 
求证:
(1)△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
【答案】
(1)证明:∵∠BAC=∠DAE=90°
∴∠BAC+∠CAD=∠DAE+CAD
即∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△BAD≌△CAE(SAS)
(2)BD、CE特殊位置关系为BD⊥CE.
证明如下:由(1)知△BAD≌△CAE,
∴∠ADB=∠E.
∵∠DAE=90°,
∴∠E+∠ADE=90°.
∴∠ADB+∠ADE=90°.
即∠BDE=90°.
∴BD、CE特殊位置关系为BD⊥CE
【解析】要证(1)△BAD≌△CAE,现有AB=AC,AD=AE,需它们的夹角∠BAD=∠CAE,而由∠BAC=∠DAE=90°很易证得.(2)BD、CE有何特殊位置关系,从图形上可看出是垂直关系,可向这方面努力.要证BD⊥CE,需证∠BDE=90°,需证∠ADB+∠ADE=90°可由直角三角形提供.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】小丽想用一块面积为900 cm2的正方形纸片,沿着边的方向裁出一块面积为600 cm2的长方形纸片,使它的长宽之比为4∶3,她不知道是否裁得出来,正在发愁,小明见了说:“别发愁,一定能用这块正方形纸片裁出需要的长方形纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图1.
①若∠AOC=60°,求∠DOE的度数;
②若∠AOC=α,直接写出∠DOE的度数(用含α的式子表示);
(2)将图1中的∠DOC绕点O顺时针旋转至图2的位置,试探究∠DOE和∠AOC的度数之间的关系,写出你的结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
一艘船从甲码头到乙码头顺流而行,用了2.5h;从乙码头返回甲码头逆流而行,用了3h.已知水流的速度是3.5km/h,求船在静水中的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(分类讨论思想)已知直线l是线段AB的垂直平分线,点M,N是直线l上的两点,如果∠NBA=15°,∠MBA=45°,则∠MAN=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
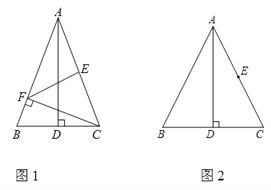
【题目】在锐角△ABC中,AB=AC,AD为BC边上的高,E为AC中点.
(1)如图1,过点C作CF⊥AB于F点,连接EF.若∠BAD=20°,求∠AFE的度数;
(2)若M为线段BD上的动点(点M与点D不重合),过点C作CN⊥AM于N点,射线EN,AB交于P点.
①依题意将图2补全;
②小宇通过观察、实验,提出猜想:在点M运动的过程中,始终有∠APE=2∠MAD.
小宇把这个猜想与同学们进行讨论,形成了证明该猜想的几种想法:
想法1:连接DE,要证∠APE=2∠MAD,只需证∠PED=2∠MAD.
想法2:设∠MAD=α,∠DAC=β,只需用α,β表示出∠PEC,通过角度计算得∠APE=2α.
想法3:在NE上取点Q,使∠NAQ=2∠MAD,要证∠APE=2∠MAD,只需证△NAQ∽△APQ.……
请你参考上面的想法,帮助小宇证明∠APE =2∠MAD.(一种方法即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com