练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】(分类讨论思想)已知直线l是线段AB的垂直平分线，点M，N是直线l上的两点，如果∠NBA＝15°，∠MBA＝45°，则∠MAN＝________.

    【答案】30°或60°

    【解析】

    根据线段垂直平分线的性质定理可知，MA＝MB，NA＝NB，

    所以∠MAB＝∠MBA＝45°，∠NAB＝∠NBA＝15°，

    当点M，N在线段AB的同侧时，∠MAN＝∠MAB－∠NAB＝45°－15°＝30°；

    当点M，N在线段AB的异侧时，∠MAN＝∠MAB＋∠NAB＝45°＋15°＝60°.

    故答案为30°或60°.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

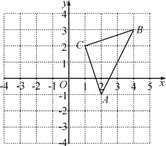
    【题目】如图，平面直角坐标系中，三角形ABC的顶点都在网格上，平移三角形ABC，使点C与坐标原点O重合．

    （1）请写出图中点A，B，C的坐标；

    （2）画出平移后的三角形OA1B1；

    （3）求三角形OA1A的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）

    A.CB=CD
    B.∠BAC=∠DAC
    C.∠BCA=∠DCA
    D.∠B=∠D=90°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于x的一元二次方程kx2+2x﹣1=0有两个不相等的实数根，则k的取值范围是（ ）
    A.k＞﹣1
    B.k＞1
    C.k≠0
    D.k＞﹣1且k≠0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在△ABC、△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C、D、E三点在同一直线上，连接BD．

    求证：
    （1）△BAD≌△CAE；
    （2）试猜想BD、CE有何特殊位置关系，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料：
    分解因式：x2+2x﹣3
    解：原式=x2+2x+1﹣4=（x+1）2﹣4
    =（x+1+2）（x+1﹣2）=（x+3）（x﹣1）
    此种方法抓住了二次项和一次项的特点，然后加一项，使这三项成为完全平方式，我们把这种分解因式的方法叫配方法．请仔细体会配方法的特点，然后尝试用配方法解决下列问题：
    （1）分解因式x2﹣2x﹣3=；a2﹣4ab﹣5b2=；
    （2）无论m取何值，代数式m2+6m+13总有一个最小值，请你尝试用配方法求出它的最小值；
    （3）观察下面这个形式优美的等式：a2+b2+c2﹣ab﹣bc﹣ca= [（a﹣b）2+（b﹣c）2+（c﹣a）2]
    该等式从左到右的变形，不仅保持了结构的对称性，还体现了数学的和谐、简洁美．
    请你说明这个等式的正确性．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等腰△ABC的周长为19，底边BC=5，AB的垂直平分线DE交AB于点D，交AC于点E，则△BEC的周长为（ ）

    A.9
    B.10
    C.11
    D.12

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个纸盒里装有四张除数字以外完全相同卡片，四张卡片上的数字分别为1，2，3，4．先从纸盒里随机取出一张，记下数字为，再从剩下的三张中随机取出一张，记下数字为，这样确定了点P的坐标（， ）．

    （1）请你运用画树状图或列表的方法，写出点Ｐ所有可能的坐标；

    （2）求点P（， ）在函数＝－＋4图象上的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，BC为弦，D为的中点，AC，BD相交于E点，过点A作⊙O的切线交BD的延长线于P点．

    （1）求证：∠PAC=2∠CBE；

    （2）若PD=m，∠CBE=α，请写出求线段CE长的思路．

    查看答案和解析>>

    同步练习册答案