
【题目】如图,AB是⊙O的直径,BC为弦,D为![]() 的中点,AC,BD相交于E点,过点A作⊙O的切线交BD的延长线于P点.
的中点,AC,BD相交于E点,过点A作⊙O的切线交BD的延长线于P点.

(1)求证:∠PAC=2∠CBE;
(2)若PD=m,∠CBE=α,请写出求线段CE长的思路.
【答案】(1)证明见解析; (2)思路见解析.
【解析】(1)证明:∵D为![]() 的中点
的中点
,
∴∠CBA=2∠CBE.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠1+∠CBA=90°.
∴∠1+2∠CBE =90°.
∵AP是⊙O的切线,
∴∠PAB=∠1+∠PAC=90°.
∴∠PAC =2∠CBE.
(2)思路:①连接AD,由D是![]() 的中点,∠2=∠CBE,
的中点,∠2=∠CBE,
由∠ACB=∠PAB=90°,得∠P=∠3=∠4,故AP=AE;
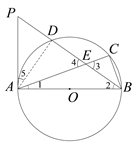
②由AB是⊙O的直径,可得∠ADB=90°;由AP=AE,
得PE=2PD=2m,∠5=![]() ∠PAC =∠CBE=
∠PAC =∠CBE= ![]()
③在Rt△PAD中,由PD=m,∠5= ![]() ,可求PA的长;
,可求PA的长;
④在Rt△PAB中,由PA的长和∠2= ![]() ,可求BP的长;
,可求BP的长;
由![]() 可求BE的长;
可求BE的长;
⑤在Rt△BCE中,由BE的长和![]() ,可求CE的长.
,可求CE的长.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(分类讨论思想)已知直线l是线段AB的垂直平分线,点M,N是直线l上的两点,如果∠NBA=15°,∠MBA=45°,则∠MAN=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
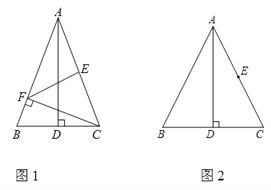
【题目】在锐角△ABC中,AB=AC,AD为BC边上的高,E为AC中点.
(1)如图1,过点C作CF⊥AB于F点,连接EF.若∠BAD=20°,求∠AFE的度数;
(2)若M为线段BD上的动点(点M与点D不重合),过点C作CN⊥AM于N点,射线EN,AB交于P点.
①依题意将图2补全;
②小宇通过观察、实验,提出猜想:在点M运动的过程中,始终有∠APE=2∠MAD.
小宇把这个猜想与同学们进行讨论,形成了证明该猜想的几种想法:
想法1:连接DE,要证∠APE=2∠MAD,只需证∠PED=2∠MAD.
想法2:设∠MAD=α,∠DAC=β,只需用α,β表示出∠PEC,通过角度计算得∠APE=2α.
想法3:在NE上取点Q,使∠NAQ=2∠MAD,要证∠APE=2∠MAD,只需证△NAQ∽△APQ.……
请你参考上面的想法,帮助小宇证明∠APE =2∠MAD.(一种方法即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将正比例函数y=kx(k>0)的图象向上平移一个单位,那么平移后的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)有4张桌子,用第一种摆设方式,可以坐 人;用第二种摆设方式,可以坐 人;
(2)有n张桌子,用第一种摆设方式可以坐 人;用第二种摆设方式,可以坐 人(用含有n的代数式表示);
(3)一天中午,餐厅要接待120位顾客共同就餐,但餐厅中只有30张这样的长方形桌子可用,且每6张拼成一张大桌子,若你是这家餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读解题过程,回答问题.
如图,OC在∠AOB内,∠AOB和∠COD都是直角,且∠BOC=30°,求∠AOD的度数.
解:过O点作射线OM,使点M,O,A在同一直线上.
因为∠MOD+∠BOD=90°,∠BOC+∠BOD=90°,所以∠BOC=∠MOD,
所以∠AOD=180°-∠BOC=180°-30°=150°.
(1)如果∠BOC=60°,那么∠AOD等于多少度?如果∠BOC=n°,那么∠AOD等于多少度?
(2)如果∠AOB=∠DOC=x°,∠AOD=y°,求∠BOC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com