
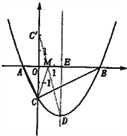
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.

【答案】(1)![]() , D (
, D (![]() ,
,![]() );(2)△ABC是直角三角形,证明见解析;
);(2)△ABC是直角三角形,证明见解析;
(3)M(![]() ,0).
,0).
【解析】(1)∵点A(-1,0)在抛物线y=![]() x2 + bx-2上,
x2 + bx-2上,
∴![]() × (-1 )2 + b× (-1)–2 = 0,
× (-1 )2 + b× (-1)–2 = 0,
![]() 解得b =
解得b =![]() ,
,
∴ 抛物线的解析式为y=![]() x2-
x2-![]() x-2.
x-2.
y= ( x2 -3x- 4 ) =![]() (x-)2-
(x-)2-![]() ,
,
∴顶点D的坐标为 (![]() , -
, -![]() ).
).
(2)当x = 0时y = -2,
∴C(0,-2),OC = 2。
当y = 0时, ![]() x2-
x2-![]() x-2 = 0,
x-2 = 0,
∴x1 =-1, x2 = 4,
∴B (4,0)
∴OA = 1, OB = 4, AB = 5.
∵AB2 = 25, AC2 = OA2 + OC2 = 5, BC2 = OC2 + OB2 = 20,
∴AC2 +BC2 = AB2.
∴△ABC是直角三角形.
(3)作出点C关于x轴的对称点C′,则C′(0,2),OC′=2,连接C′D交x轴于点M,根据轴对称性及两点之间线段最短可知,MC + MD的值最小及△DCM的周长最小
设抛物线的对称轴交x轴于点E.
∵ED∥y轴, ∴∠OC′M=∠EDM,∠C′OM=∠DEM
∴△C′OM∽△DEM.
∴![]()
∴![]() , ∴m =
, ∴m =![]() .
.
所以M的坐标为(![]() ,0)
,0)


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】在一个纸盒里装有四张除数字以外完全相同卡片,四张卡片上的数字分别为1,2,3,4.先从纸盒里随机取出一张,记下数字为![]() ,再从剩下的三张中随机取出一张,记下数字为
,再从剩下的三张中随机取出一张,记下数字为![]() ,这样确定了点P的坐标(
,这样确定了点P的坐标(![]() ,
, ![]() ).
).
(1)请你运用画树状图或列表的方法,写出点P所有可能的坐标;
(2)求点P(![]() ,
, ![]() )在函数
)在函数![]() =-
=-![]() +4图象上的概率.
+4图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC为弦,D为![]() 的中点,AC,BD相交于E点,过点A作⊙O的切线交BD的延长线于P点.
的中点,AC,BD相交于E点,过点A作⊙O的切线交BD的延长线于P点.

(1)求证:∠PAC=2∠CBE;
(2)若PD=m,∠CBE=α,请写出求线段CE长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
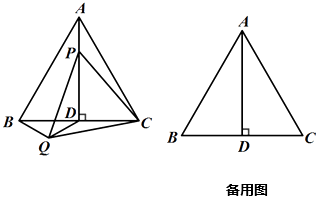
【题目】如图,正△ABC 中,高线 ![]() ,点
,点 ![]() 从点
从点 ![]() 出发,沿着
出发,沿着 ![]() 运动到点
运动到点 ![]() 停止,以
停止,以 ![]() 为边向左下方作正
为边向左下方作正 ![]() ,连接
,连接 ![]() ,
, ![]() .
.
(1)求证: ![]() ≌
≌ ![]() ;
;
(2)在点P的运动过程中,当 ![]() 是等腰三角形时,求
是等腰三角形时,求 ![]() 的度数;
的度数;
(3)直接写出在点 P的运动过程中, ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
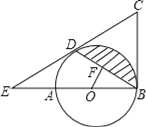
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=2,∠A=70°,以BC边为直径作⊙O,分别交AB,AC于点D,E,连接DO,EO,则S扇形OBD+S扇形OEC= . (结果用π表示) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com