
| 销售量p(件) | p=40-x |
| 销售单价q(元/件) | 当1≤x≤20时,q=40+$\frac{1}{2}$x; 当21≤x≤50时,q=30+$\frac{525}{x}$ |
分析 (1)在每个x的取值范围内,令q=45,分别解出x的值即可;
(2)利用利润=(售价-成本)×销售数量,分别求出在1≤x≤20和21≤x≤40时,y与x的函数关系式,然后再确定出函数的最值即可;
(3)当1≤x≤20时,每天的利润y=$-{\frac{1}{2}x}^{2}+(10-m)x+400+40m$,然后根据x=-$\frac{b}{2a}$≤7求解即可.
解答 解:(1)当1≤x≤20时,令40+$\frac{1}{2}$x=45,得x=10,
当21≤x≤40时,令30+$\frac{525}{x}$=45,
解得:x=35,
经检验得x=35是原方程的解且符合题意,
答:第10天或者第35天该商品的销售单价为45元/件.
(2)当1≤x≤20时,y=(40+$\frac{1}{2}$x-30)(40-x)=-$\frac{1}{2}$x2+10x+400,
当x=-$\frac{b}{2a}$=10时,y有最大值,最大值=$-\frac{1}{2}×1{0}^{2}+10×10+400$=450元.
当21≤x≤40时,y=(30+$\frac{525}{x}$-30)(40-x)=$\frac{21000}{x}$-525,
当x=21时,有最大值,最大值为y=$\frac{21000}{21}-525$=475.
综上所述,第21天获得的利润最大,最大利润是475元.
(3)由题意可知每天的利润y=-$\frac{1}{2}$x2+10x+400+m(40-x)=$-{\frac{1}{2}x}^{2}+(10-m)x+400+40m$,
∵前7天中,每天获得奖励后的利润随时间x(天)的增大而增大,
∴-$\frac{b}{2a}$≥7,即:-$\frac{10-m}{2×(-\frac{1}{2})}$≥7.
解得:m≤3.
∴m的取值范围是2≤m≤3.
点评 本题主要考查的是二次函数的应用,根据题意列出函数关系式是解题的关键.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源:2017届四川省遂宁市九年级上学期期末考试数学试卷(解析版) 题型:单选题
二次函数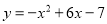 ,当
,当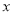 取值为
取值为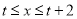 时,有最大值
时,有最大值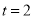 ,则
,则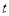 的取值范围为( )
的取值范围为( )
A. 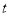 ≤0 B. 0≤
≤0 B. 0≤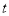 ≤3 C.
≤3 C. 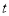 ≥3 D. 以上都不对
≥3 D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
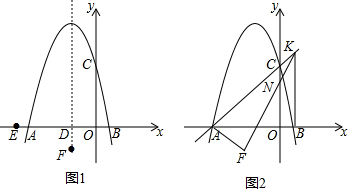
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -5 | B. | -$\frac{5}{2}$ | C. | $\frac{5}{2}$ | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com