
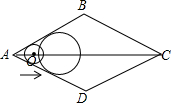
 如图:菱形ABCD中,∠BAD:∠ADC=1:2,对角线AC=20,点O沿A点以1cm/s的速度运动到C点(不与C重合),以O为圆心的圆始终保持与菱形的两边相切,设⊙O的面积为S,则S与点O运动的时间t的函数图象大致为( )
如图:菱形ABCD中,∠BAD:∠ADC=1:2,对角线AC=20,点O沿A点以1cm/s的速度运动到C点(不与C重合),以O为圆心的圆始终保持与菱形的两边相切,设⊙O的面积为S,则S与点O运动的时间t的函数图象大致为( )| A. | 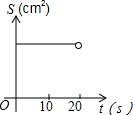 | B. | 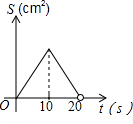 | C. |  | D. | 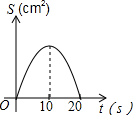 |
分析 由图可知:分段考虑,当点O由点A到达AC的中点时,当点O到达AC的中点时,当点O由AC的中点到点C时,分别列出函数解析式,进一步利用函数的性质判断图象即可.
解答 解:当点O由点A到达AC的中点时,圆的面积为S=π($\frac{t}{2}$)2=$\frac{π}{4}$t2(0<t<10);
当点O到达AC的中点时,圆的面积为S=$\frac{π}{4}$t2(t=10)最大;
当点O由AC的中点到点C时,圆的面积为S=π[$\frac{1}{2}$(t-10)2]=$\frac{π}{4}$(t-10)2(10<t<20);
由此可知符合函数图象是C.
故选:C.
点评 此题考查动点问题的函数图象,分段考虑,求得函数解析式,利用函数的性质得出图象是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 日 期 | 28 | 29 | 30 | 1 | 2 | 3 |
| 水位记录 | +0.7 | +0.4 | -0.9 | -0.6 | +0.1 | -0.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x2-1 | B. | y=x2+1 | C. | y=(x-1)2 | D. | y=(x+1)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
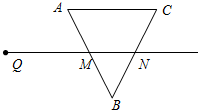 如图,射线QN与边长为8的等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN.动点P从点Q出发,沿射线QN以每秒2cm的速度向右移动,以点P为圆心,2$\sqrt{3}$cm为半径的圆也随之移动.若AM=MB=4cm,QM=8cm,且经过t秒,当⊙P与△ABC的边相切时,则t可取的一切值为t=2或3≤t≤7或t=8(单位:秒).
如图,射线QN与边长为8的等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN.动点P从点Q出发,沿射线QN以每秒2cm的速度向右移动,以点P为圆心,2$\sqrt{3}$cm为半径的圆也随之移动.若AM=MB=4cm,QM=8cm,且经过t秒,当⊙P与△ABC的边相切时,则t可取的一切值为t=2或3≤t≤7或t=8(单位:秒).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
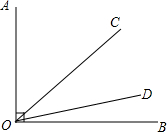 如图,已知∠AOB=90°,射线OC绕点O从OA位置开始,以每秒4°的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1°的速度逆时针方向旋转.当OC与OA成180°时,OC与OD同时停止旋转.
如图,已知∠AOB=90°,射线OC绕点O从OA位置开始,以每秒4°的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1°的速度逆时针方向旋转.当OC与OA成180°时,OC与OD同时停止旋转.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3+3=-6 | B. | -6÷2×3=-1 | C. | -9÷(-1$\frac{1}{2}$)2=-4 | D. | -4+(-2)×$\frac{1}{2}$=-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com