
 ,1,
,1, ,2,
,2, ,3,
,3, ,4,
,4, ,5,可得函数图象上的十个点.在这十个点中随机取两个点P(x1,y1),Q(x2,y2),则P,Q两点在同一反比例函数图象上的概率是________.
,5,可得函数图象上的十个点.在这十个点中随机取两个点P(x1,y1),Q(x2,y2),则P,Q两点在同一反比例函数图象上的概率是________.
 与
与 ;1与2;
;1与2; 与
与 ;2与3时的两点在同一反比例函数图象上,而
;2与3时的两点在同一反比例函数图象上,而 与
与 和
和 与
与 又为两种情况,所以满足题意的情况有8种,让8除以90即为所求的概率.
又为两种情况,所以满足题意的情况有8种,让8除以90即为所求的概率. ,-
,- );(1,-4);(
);(1,-4);( ,-
,- );(2,-3);(
);(2,-3);( ,-
,- );(3,-2);(
);(3,-2);( ,-
,- );(4,-1);(
);(4,-1);( ,-
,- );(5,0),第一个点的选取有10种情况,那么第二个点有9种情况,共有10×9=90种情况;在同一反比例函数上的有点(
);(5,0),第一个点的选取有10种情况,那么第二个点有9种情况,共有10×9=90种情况;在同一反比例函数上的有点( ,-
,- )与(
)与( ,-
,- );(1,-4)与(4,-1);P(
);(1,-4)与(4,-1);P( ,-
,- )与(
)与( ,-
,- );(2,-3)与(3,-2)各2种情况共8种情况,
);(2,-3)与(3,-2)各2种情况共8种情况,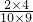 =
=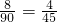 .
. .
.

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com