
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8. 
(1)用直尺和圆规在边BC上求作一点P,使P到C的距离与P到AB的距离相等(不写作法,保留作图痕迹);
(2)连结AP,求AP的长.
【答案】
(1)解:如图,点P即为所求 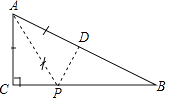
(2)】解:在Rt△ABC中,∵AB2=AC2+BC2=62+82=100,
∴AB=6.
∵PC⊥AC,PD⊥AB,
∴PC=PD,
在Rt△ACP与Rt△ADP中,
∵ ![]() ,
,
∴Rt△ACP≌Rt△ADP(HL),
∴AD=AC=6,BD=AB﹣AD=4.
设CP=PD=x,则PB=BC﹣PC=8﹣x;
在Rt△BDP中,∵PB2=PD2+BD2,
∴(8﹣x)2=x2+42,x=3,
∴PC=3,
在Rt△ACP中,
∵AP2=AC2+PC2=62+32=45,
∴AP=3 ![]() .
.
【解析】(1)作∠A的平分线交BC于点P即可;(2)先根据勾股定理求出AB的长,根据HL定理得出Rt△ACP≌Rt△ADP,故可得出AD,BD的长,设CP=PD=x,则PB=BC﹣PC=8﹣x,在Rt△BDP中中根据勾股定理求出x的值,同理,在Rt△ACP中根据勾股定理求出PC的值即可.
【考点精析】掌握角平分线的性质定理和勾股定理的概念是解答本题的根本,需要知道定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】如图,将长方形ABC沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E. 
(1)试判断△BDE的形状,并说明理由;
(2)若AB=4,AD=8,求AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,将△ABC绕顶点B顺时针旋转,得到△A′BC′.设∠A=α,当A′C′恰好经过顶点C时,∠A′BC=_____(用含α的式子表示).
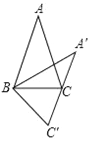
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com