
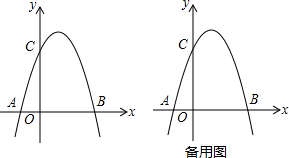
���� ��1���������߽���ʽ�õ�C��0��3k���������֪�����õ���A�����꣬�ѵ�A��������������߽���ʽ�г�����k��һԪ���η��̣�ͨ���ⷽ�����k��ֵ���ɣ�
��2������ƽ���ߵ��ж���֪AE��GH��BF������ƽ���߷��߶γɱ����õ���$\frac{AH}{BH}$=$\frac{EG}{FG}$=1���ɵ��������ͼ�ε��������H��1��0��������ΪDH��y�ᣬ���Ե�D�ĺ�����Ϊ1���ѵ�D�ĺ�������뺯������ʽ������õ�D�������ꣻ
��3����P��m��-m2+2m+3�������������ϵ�����������ʹ���ϵ�������ֱ��PA�Ľ���ʽΪy=��3-m��x+3-m����NH=6-2m��ͬ������ֱ��PB�Ľ���ʽ�õ�MH=2m+2�����MD=NH�����P��2��3������ͼ2����P��PK��AB��K�������Ƚǡ�QPA=��BPK������ͨ����Rt��PKB�õ���tan��BPK=$\frac{BK}{PK}$=$\frac{1}{3}$����tan��QPA=$\frac{1}{3}$��
��� ��1���⣺��x=0ʱ��y=-02+2k��0+3k��
���y=3k��
��C��0��3k����
��OC=3k��
��OA=$\frac{1}{3}$OC��
��OA=k��
��A��-k��0����
�ߵ�A���������ϣ�
��0=-��-k��2+2k����-k��+3k��
���k1=0����ȥ����k2=1��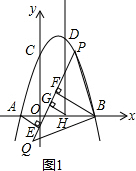
�������ߵĽ���ʽΪy=-x2+2x+3��
��2���⣺��ͼ1���������ߵĽ���ʽΪy=-x2+2x+3��
�൱y=0ʱ��0=-x2+2x+3��
���x1=-1��x2=3��
��A��-1��0��B��3��0����
��OA=1��OB=3��
��AB=OA+OB=4��
��AE��PQ��BF��PQ��
���AEP=��BFQ=90�㣬
��AE��BF��
��GH��ֱƽ��EF��
��EG=FG����HGQ=90�㣬
���HGQ=��BFQ��
��GH��BF��
��AE��GH��BF��
��$\frac{AH}{BH}$=$\frac{EG}{FG}$=1��
��AH=BH=$\frac{1}{2}$AB=2��
��OH=OB-BH=1��
��H��1��0����
��DH��y�ᣬ
���D�ĺ�����Ϊ1��
�ߵ�D���������ϣ�
�൱x=1ʱ��y=-12+2��1+3=4��
��D��1��4����
��3���⣺�ߵ�P��������y=-x2+2x+3�ϣ���P��m��-m2+2m+3��
�ɣ�2��֪A��-1��0��B��3��0����ֱ��PA�Ľ���ʽΪy=k1x+b1
��A��-1��0����P��m��-m2+2m+3����ֱ��PA�ϣ���
$\left\{\begin{array}{l}{0=-1��{k}_{1}+{b}_{1}}\\{-{m}^{2}+2m+3=m��{k}_{1}+{b}_{1}}\end{array}\right.$��
���$\left\{\begin{array}{l}{{k}_{1}=3-m}\\{{b}_{1}=3-m}\end{array}\right.$��
��ֱ��PA�Ľ���ʽΪy=��3-m��x+3-m��
��N�ĺ�����Ϊ1
�൱x=1ʱ��y=��3-m����1+3-m=6-2m��
��NH=6-2m��
��ֱ��PB�Ľ���ʽΪy=k2x+b2��k2��0����
��B��3��0����P��m��-m2+2m+3����ֱ��PB�ϣ���
$\left\{\begin{array}{l}{0=3��{k}_{2}+{b}_{2}}\\{-{m}^{2}+2m+3=m��{k}_{2}+{k}_{2}}\end{array}\right.$��
���$\left\{\begin{array}{l}{{k}_{2}=-m-1}\\{{b}_{2}=3m+3}\end{array}\right.$��
��ֱ��PB�Ľ���ʽΪy=��-m-1��x+3m+3��
��M�ĺ�����Ϊ1��
�൱x=1ʱ��y=��-m-1����1+3m+3=2m+2��
��MH=2m+2��
��D��1��4����
��DH=4��
��MD=MH-DH=2m-2��
��MD=NH��
��2m-2=6-2m��
���m=2��
��P��2��3����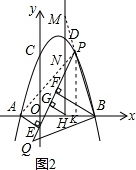
��ͼ2����P��PK��AB��K��
��OK=2��PK=3��
��AK=OA+OK=3��BK=OB-OK=1��
��AK=PK=3��
��PK��AB��
���PKA=90�㣬
���PAK=��APK=45�㣮
��BP=BQ����PBQ=90�㣬
���BPQ=��BQP=45��
���APK-��QPK=��QPB-��QPK������QPA=��BPK��
��Rt��PKB��tan��BPK=$\frac{BK}{PK}$=$\frac{1}{3}$��
��tan��QPA=$\frac{1}{3}$��
���� �������ؿ����˴���ϵ��������κ�����һ�κ�������ʽ��ͼ����ת�任��ƽ���ߵ��ж������ʵ���Ҫ֪ʶ�㣬�ۺ���ǿ������Ҫ�ߣ�����ѧ�������������ν�ϵ���ѧ˼�뷽����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com