练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．科学研究表明，当人的下肢与身高比为0.618时，看起来最美，某成年女士身高为160cm，下肢长为98cm，该女士穿的高跟鞋鞋跟的最佳高度约为2.3cm（精确到0.1cm）．

    分析 设该女士穿的高跟鞋鞋跟的最佳高度为xcm，根据黄金比的概念列出方程，解方程即可．

    解答 解：设该女士穿的高跟鞋鞋跟的最佳高度为xcm，
    由题意得，$\frac{98+x}{160+x}$=0.618，
    解得x≈2.3．
    故答案为：2.3．

    点评 本题考查的是黄金分割的概念，把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值$\frac{\sqrt{5}-1}{2}$叫做黄金比．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    8．①a的倒数是$\frac{1}{a}$；②0的倒数是0；③若ab=1则a与b互为倒数．以上正确的说法是③（请填上正确的序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知抛物线y=-x2+2kx+3k与x轴交于A、B两点，与y轴交于点C，且OA=$\frac{1}{3}$OC．
    （1）求此抛物线的解析式；
    （2）若点P为抛物线上第一象限内一点，连接BP，将线段BP绕点B逆时针旋转90°，得到BQ，连接PQ，过A作直线PQ的垂线，垂足为E，过B作直线PQ的垂线，垂足为F，作线段EF的垂直平分线交x轴于点H，过点H作HD∥y轴，交抛物线于点D，求点D的坐标；
    （3）在（2）的条件下，延长BP交HD延长线于点M，连接AP交HD于点N，当MD=NH时，求∠QPA的正切值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．大于-1而小于$\sqrt{15}$的整数是（　　）
    A．0、1、2、3B．1、2、3C．2、3、4D．0、1、2、3、4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．一个机器人从某地Q出发，向东走了4米到达A处，继续走了2米到达B处，又向西走了10米到达C处，最后向东走了4米．
    （1）若以出发点Q为原点，以向东的方向为正方向，用1个单位长度表示1米，试在数轴上表示出A、B、C处的位置？
    （2）你能判断机器人最后的位置吗？
    （3）机器人离开出发点Q最远时的距离是多少米？
    （4）B处与C处之间的距离是多少米？
    （5）机器人共走了多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

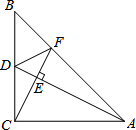    3．已知，在△ABC中，AC=BC，∠ACB=90°，AD是中线，CE⊥AD交AB于点F，垂足为E，连接DF，则结论①∠BDF=∠ADC；②∠BFD=∠AFC；③CF+DF=AD．其中结论正确的个数是（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

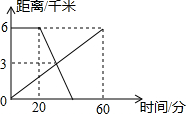    2．已知A、B两地相距4千米，上午8：00，甲从A地出发步行到B地，8：20乙从B地出发骑自行车到A地，甲乙两人离A地的距离y（千米）与甲所用的时间X（分）之间的关系如图所示，由图中的信息可知：
    （1）请直接写出甲离A地的距离y（千米）与甲所用的时间x（分）之间的关系式；
    （2）求乙离A地的距离y（千米）与甲所用的时间x（分）之间的关系式并直按写出乙到达A地的时间为20；
    （3）直接写出甲出发后多长时间两人相距2千米？25分钟或35分钟．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．化简或求值：
    （1）9a-8b-2a+5b；                
    （2）3a2-[5a-（$\frac{1}{2}$a-3）+2a2]；
    （3）2（x2y+xy）-3（x2y-xy）-4x2y，其中x=-2，y=$\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

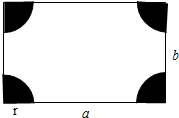    20．如图，在一长方形休闲广声场的四角都设计一块半径相同的四分之一圆的花坛，若圆形的半径为r米，广场的长为a米，宽为b米．
    （1）请用代数式表示广场空地的面积；
    （2）若休闲广场的长为400米，宽为200米，圆形花坛的半径为10米，求广场空地的面积（计算结果保留π）．

    查看答案和解析>>

    同步练习册答案