
分析 (1)根据题中给出的列子可直接得出结论;
(2)分别计算出$\frac{1}{1×3}$,$\frac{1}{3×5}$,$\frac{1}{5×7}$的值,再进行计算即可;
(3)根据(1)、(2)的结论找出规律,并进行计算即可.
解答 解:(1)∵$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,
∴$\frac{1}{2007×2008}$=$\frac{1}{2007}$-$\frac{1}{2008}$.
故答案为:$\frac{1}{2007}$-$\frac{1}{2008}$;
(2)∵$\frac{1}{1×3}$=$\frac{1}{3}$=$\frac{1}{2}$(1-$\frac{1}{3}$),$\frac{1}{3×5}$=$\frac{1}{15}$=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$),$\frac{1}{5×7}$=$\frac{1}{35}$=$\frac{1}{2}$($\frac{1}{5}$-$\frac{1}{7}$),
∴$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{2006×2007}$
=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{2006}$-$\frac{1}{2007}$)
=$\frac{1}{2}$(1-$\frac{1}{2007}$)
=$\frac{1003}{2007}$.
故答案为:$\frac{1003}{2007}$;
(3)根据(1),(2)的计算,我们可以猜测下列结论:$\frac{1}{n(n+k)}$=$\frac{1}{k}$($\frac{1}{n}$-$\frac{1}{n+k}$).
$\frac{1}{1×4}$+$\frac{1}{4×7}$+$\frac{1}{7×10}$+…+$\frac{1}{2005×2008}$=$\frac{1}{3}$(1-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{7}$+$\frac{1}{7}$-$\frac{1}{10}$+…+$\frac{1}{2005}$-$\frac{1}{2008}$)=$\frac{669}{2008}$.
故答案为:$\frac{1}{k}$($\frac{1}{n}$-$\frac{1}{n+k}$).
点评 本题考查的是有理数的混合运算,根据题意找出规律是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
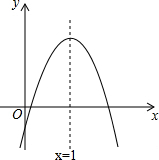 二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b<0;②c<0;③4a+2b+c>0;④(a+c)2<b2;⑤b+2a=0;其中正确的是①②④⑤(填序号)
二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b<0;②c<0;③4a+2b+c>0;④(a+c)2<b2;⑤b+2a=0;其中正确的是①②④⑤(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
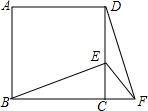 如图,正方形ABCD中,E为CD上一点,F为BC延长线上一点,CE=CF.
如图,正方形ABCD中,E为CD上一点,F为BC延长线上一点,CE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
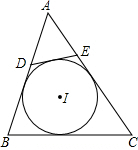 如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为21,BC边的长为6,△ADE的周长为9.
如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为21,BC边的长为6,△ADE的周长为9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com