Question

【题目】如图，直线l：y=kx+b（k＜0）与函数（x＞0）的图象相交于A、C两点，与x轴相交于T点，过A、C两点作x轴的垂线，垂足分别为B、D，过A、C两点作y轴的垂线，垂足分别为E、F；直线AE与CD相交于点P，连接DE，设A、C两点的坐标分别为（a，）、（c，），其中a＞c＞0．

（1）如图①，求证：∠EDP=∠ACP；

（2）如图②，若A、D、E、C四点在同一圆上，求k的值；

（3）如图③，已知c=1，且点P在直线BF上，试问：在线段AT上是否存在点M，使得OM⊥AM？请求出点M的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）证明见解析；（2）-1；（3）（，）．

【解析】

试题分析：（1）由P、E、D的坐标可表示出PA、EP、PC和DP的长，可证明△EPD∽△CPA，利用相似三角形的性质可证得结论；

（2）连接AD、EC，可证明△AEC≌△CDA，可得CD=AE，把A、C坐标代入直线l解析式，可求得k的值；

（3）假设在线段AT上存在点M，使得OM⊥AM，连接OM、OA，可表示出C、F、P、B的坐标，利用直线BF的解析式可求得a的值，可求得A点坐标，可求得T点坐标，在△OAT中，利用等积法可求得OM的长，在RtOMT中可求得MT的长，作MN⊥x轴，同理可求得MN的长，则可求得ON的长，可判断N在线段BT上，满足条件，从而可知存在满足条件的M点．

试题解析：（1）证明：

由题意可知P（c，），E（0，），D（c，0），∴PA=a﹣c，EP=c，PC=﹣=，DP=，∴，且∠EPD=∠APC，∴△EPD∽△CPA，∴∠EDP=∠ACP；

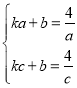（2）解：如图1，连接AD、EC，由（1）可知DE∥AC，∴∠DEC+∠ECA=180°，∵A、D、E、C四点在同圆周上，∴∠DEC+∠DAC=180°，∴∠ECA=∠DAC，在△AEC和△CDA中，∵∠ECA=∠DAC，∠AEC=∠CDA，AC=CA，∴△AEC≌△CDA（AAS），∴CD=AE，即a=，可得ac=4，∵A、C在直线l上，∴，解得k==﹣=﹣1；

（3）假设在线段AT上存在点M，使OM⊥AM，连接OM、OA，作MN⊥x轴于点N，如图2，∵c=1，∴C（1，4），F（0，4），P（1，），B（a，0），设直线BF的解析式为y=k′x+4，由题意可得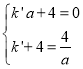：，解得a=2，∴A（2，2），∴AP为△DCT的中位线，∴T（3，0），∴AT= =

∵S△OAT=OTAB=ATOM，∴OM===，在Rt△OMT中，MT= = =，同理可求得MN==，在Rt△OMN中，ON= = =，∵2＜＜3，∴点M在线段AT上，即在线段AT上存在点M，使得OM⊥AM，M点的坐标为（，）．