练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列计算正确的是（　　）

    A.a2+3a2＝4a4B.a2b2b3＝2a6b

    C.（6a3b2）÷（3a）＝2a2D.（﹣3a）2＝9a2

    【答案】D

    【解析】

    直接利用整式的混合运算法则分别判断得出答案．

    解：A、a2+3a2＝4a2，故此选项不合题意；

    B、a2b2b3＝2a2b4，故此选项不合题意；

    C、（6a3b2）÷（3a）＝2a2b2，故此选项不合题意；

    D、（﹣3a）2＝9a2，故此选项符合题意；

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某天襄阳某镇观赏桃花的游客近16000人，数据16000用科学记数法表示为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，△DEF是由△ABC平移得到的，点A（﹣1，﹣4）的对应点为D（1，﹣1），则点B（1，1）的对应点F的坐标为（ ）
    A.（2，2）
    B.（3，4）
    C.（﹣2，2）
    D.（2，﹣2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒个单位长度，则第2015秒时，点P的坐标是（ ）

    A．（2014，0） B．（2015，﹣1） C．（2015，1） D．（2016，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法中正确的是（　　）

    A. ﹣a表示负数 B. 近似数9.7万精确到十分位

    C. 一个数的绝对值一定是正数 D. 最大的负整数是﹣1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学老师布置了这样一道作业题：
    在△ABC中，AB=AC≠BC，点D和点A在直线BC的同侧，BD=BC，∠BAC=α，∠DBC=β，α+β=120°，连接AD，求∠ADB的度数．
    小聪提供了研究这个问题的过程和思路：先从特殊问题开始研究，当α=90°，β=30°时（如图1），利用轴对称知识，以AB为对称轴构造△ABD的轴对称图形△ABD′，连接CD′（如图2），然后利用α=90°，β=30°以及等边三角形的相关知识便可解决这个问题．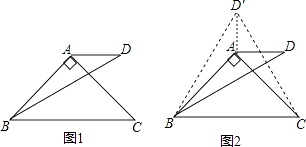

    （1）请结合小聪研究问题的过程和思路，求出这种特殊情况下∠ADB的度数；
    （2）结合小聪研究特殊问题的启发，请解决数学老师布置的这道作业题；
    （3）解决完老师布置的这道作业题后，小聪进一步思考，当点D和点A在直线BC的异侧时，且∠ADB的度数与（1）中相同，则α，β满足的条件为（直接写出结果）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列方程变形属于移项的是（ ）
    A.由﹣2y﹣5=﹣1+y，得﹣2y﹣y=5﹣1
    B.由﹣3x=﹣6，得x=2
    C.由 y=2，得y=10
    D.由﹣2（1﹣2x）+3=0，得﹣2+4x+3=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将57600000用科学记数法表示为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知a , b为常数，且三个单项式4xy2 ， axyb ， -5xy相加得到的和仍然是单项式。那么a和b的值可能是多少？说明你的理由。

    查看答案和解析>>

    同步练习册答案